Dạng 2: Góc nội tiếp- góc tạo bởi tiếp tuyến và dây cung có đáp án

34 người thi tuần này 4.6 2.9 K lượt thi 42 câu hỏi 50 phút

Câu 1

Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây MN song song với BC và gọi S là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA.

Xem đáp án

Lời giải

Trình bày lời giải

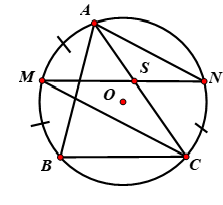
Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. (ảnh 1)

Do M là điểm chính giữa cung nhỏ AB nên sđ $\overset{⏜}{M B} =$ sđ $\overset{⏜}{M A}$

Do MN // BC nên $\hat{N M C} = \hat{M C B}$ $\Rightarrow$ sđ $\overset{⏜}{M B}$ = sđ $\overset{⏜}{N C}$

Vậy sđ sđ $\overset{⏜}{M B}$ =sđ $\overset{⏜}{N C}$

$\hat{N A S} = \hat{A N S}$ (hai góc nội tiếp cùng chắn hai cung bằng nhau)

$\hat{S M C} = \hat{S C M}$ (hai góc nội tiếp cùng chắn hai cung bằng nhau)

Vậy các tam giác ASN và MSC cân tại C

Nhận xét: Ở bài toán này học sinh có thể nhớ tới bài toán: Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau từ đó nhìn ra $\overset{⏜}{M B} = \overset{⏜}{C N}$

Câu 2

Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. Kẻ tiếp tuyến AK với đường tròn (M, MB), K là tiếp điểm. Chứng minh rằng DK vuông góc với AM.

Xem đáp án

Lời giải

Trình bày lời giải:

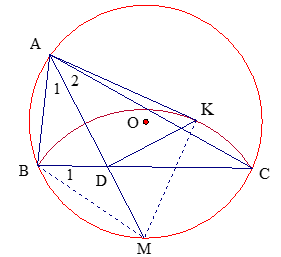
Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. (ảnh 1)

$\hat{A_{1}} = \hat{A_{2}}$ mà $\hat{B_{1}} = \hat{A_{2}}$ ( góc nội tiếp) nên $\hat{B_{1}} = \hat{A_{1}}$ .

$Δ M B D ∽ Δ M A B$ (g.g) $\Rightarrow \frac{M D}{M B} = \frac{M B}{M A} \Rightarrow \frac{M D}{M K} = \frac{M K}{M A}$

Kết hợp với $\hat{D M K} = \hat{A M K}$ (góc chung)

ta có: $Δ D M K Δ K M A$ (c.g.c) $\Rightarrow \hat{MDK} = \hat{MKA} = 90^{°}$

Vậy DK ^AM.

Câu 3

Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn tâm O, đường kính AM.

a) Tính $\hat{A C M}$ ;

Xem đáp án

Lời giải

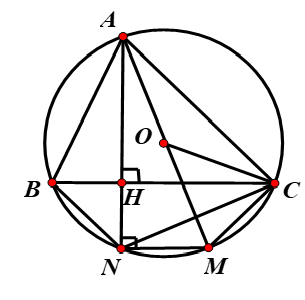
a) Ta có $\hat{A C M} = 90^{0}$ (góc nội tiếp).

Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn tâm O, đường kính AM. a) Tính góc ACM ; (ảnh 1)

Câu 4

b) Chứng minh $\hat{B A H} = \hat{O C A}$ ;

Xem đáp án

Lời giải

b) Vì $\hat{A B C} = \hat{A M C}$ (cùng chắn cung AC) và $\hat{A H B} = \hat{A C M} = 90^{0}$

Nên $Δ A B H$ và đồng dạng $Δ A M C$ ( g-g)

$\Rightarrow \begin{array}{l} \hat{B A H} = \hat{O A C} \\ \hat{O C A} = \hat{O A C} \end{array}\} \Rightarrow \hat{B A H} = \hat{O C A}$

Câu 5

c) Gọi N là giao điểm AH với đường tròn (O). Tứ giác BCMN là hình gì? Vì sao?

Xem đáp án

Lời giải

c) $\hat{A N M} = 90^{0}$ , $A N ⊥ N M$ và nên MN // BC $\Rightarrow M N B C$ là hình thang

$B C / / M N \Rightarrow$ sđ $\overset{⏜}{B N} =$ sđ $\overset{⏜}{C M}$ (xem chứng minh Bài 1)

sđ $\overset{⏜}{B N} =$ sđ $\overset{⏜}{C N} \Rightarrow B M = C N$ $\Rightarrow M N B C$ là hình thang cân.

Câu 6

Cho đường tròn tâm O và một dây AB của đường tròn đó. Các tiếp tuyến vẽ từ A và B của đường tròn cắt nhau tại C. Gọi D là một điểm trên đường tròn có đường kính OC ( D khác A và B). CD cắt cung AB của đường tròn (O) tại E. (E nằm giữa C và D). Chứng minh rằng:

a) $\hat{B E D} = \hat{D AE}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Chứng minh rằng:

b, $D E^{2} = D A . D B .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Tam giác ABC nội tiếp đường tròn tâm O. Các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Từ điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB và một cát tuyến MCD. Gọi I là giao điểm của AB và CD. Chứng minh rằng: $\frac{I C}{I D} = \frac{M C}{M D}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Gọi CA, CB lần lượt là các tiếp tuyến của đường tròn (O; R) với A, B là các tiếp điểm. Vẽ đường tròn tâm I qua C và tiếp xúc với AB tại B. Đường tròn (I) cắt đường tròn (O) tại M. Chứng minh rằng đường thẳng AM đi qua trung điểm của BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Cho hình bình hành ABCD, góc A < 90⁰. Đường tròn ngoại tiếp tam giác BCD cắt AC ở E. Chứng mình rằng BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Mỗi khẳng định sau đúng hay sai:

A. Góc tạo bởi tia tiếp tuyến và dây cung luôn nhỏ hơn 90⁰.

B. Trong một đường tròn, các góc nội tiếp bằng nhau chắn các cung bằng nhau.

C. Góc vuông nội tiếp thì chắn nửa đường tròn.

D. Góc tù nội tiếp thì có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Cho hình vẽ, biết AB là đường kính của đường tròn (O), xy là tiếp tuyến của đường tròn tại A. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

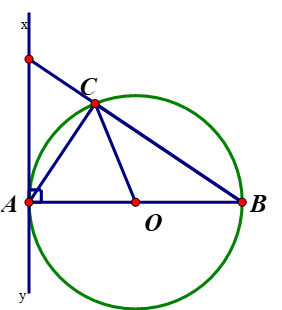
A. Góc CAx là góc tạo bởi tia tiếp tuyến và dây cung.

B. Góc BAy là góc tạo bởi tia tiếp tuyến và dây cung

C. Góc ACB là góc tù.

D. $\hat{C A x} < \hat{B C O}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Ghép mỗi ý ở cột bên trái với mỗi ý ở cột bên phải để được khẳng định đúng

A.   Góc nội tiếp là góc

1)    có số đo bằng 90⁰

B.   Góc nội tiếp chắn nửa đường tròn

2)    bằng nhau.

C.   Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì

3)    có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn.

D.   Trong một đường tròn, hai góc nội tiếp không bằng nhau, góc lớn hơn thì

4)    chắn dây lớn hơn.

5)    có cung bị chắn lớn hơn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Tam giác ABC nội tiếp (O;R). Tia phân giác của góc A cắt (O) tại M. Tia phân giác góc ngoài tại đỉnh A cắt (O) tại N. CMR:

a) Tam giác MBC cân.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

b,3 điểm M, O, N thẳng hàng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho (O) và hai dây AB, CD bằng nhau và cắt nhau tại M. ( C thuộc cung nhỏ AB, B thuộc cung nhỏ CD).

a) CMR: cung AC = cung DB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

b, CMR: ∆MAC = ∆MDB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Cho (O) và hai dây MA và MB vuông góc với nhau. Gọi I, K lần lượt là điểm chính giữa của các cung nhỏ MA, MB. Gọi P là giao điểm của AK và BI.

a) CMR: A, O, B thẳng hàng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

b, CMR: P là tâm đường tròn nội tiếp ∆MBA.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

c, Giả sử MA = 12cm, MB = 16cm, tính bán kính đường tròn nội tiếp ∆MBA.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Cho tam giác ABC nhọn nội tiếp đường tròn (O). Tia phân giác của góc A cắt (O) tại M.
a) CMR : tam giác BMC cân.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

b, CMR : góc BMC = góc ABC + góc ACB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

c, Gọi D là giao điểm của AM và BC. CMR : AB. AC = AD. AM; MD. MA = MB².

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Cho nửa đường tròn (O) đường kính CB, A thuộc nửa đường tròn sao cho AB < AC. Tiếp tuyến tại A cắt đường thẳng BC ở I. Kẻ AH vuông góc với BC. CMR:

a) AB là tia phân giác của góc IAH.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

b, IA² = IB. IC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Cho tam giác ABC vuông tại A, đường cao AH. Vẽ (I) đường kính BH cắt AB ở M. Vẽ (K) đường kính CH cắt AC ở N.

a) Tứ giác AMHN là hình gì ? CM ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

b) CMR : MN là tiếp tuyến chung của hai đường tròn (I) và (K) ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

c, Vẽ tiếp tuyến Ax của đường tròn ngoại tiếp tam giác ABC. CMR : Ax // MN.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Trên nửa đường tròn (O) đường kính AB, lấy hai điểm M và N sao cho cung AM = cung MN = cung NB. Gọi P là giao điểm của AM và BN ; H là giao điểm của AN với BM. CMR :

a) Tứ giác AMNB là hình thang cân.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Trên nửa đường tròn (O) đường kính AB, lấy hai điểm M và N sao cho cung AM = cung MN = cung NB. Gọi P là giao điểm của AM và BN ; H là giao điểm của AN với BM. CMR :

a) Tứ giác AMNB là hình thang cân.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

b, 4 điểm P, M, H, N cùng thuộc một đường tròn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

c, PH vuông góc với AB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

d, 4 điểm P, M, H, N cùng thuộc một đường tròn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Cho (O) và (O’) bằng nhau, cắt nhau tại A và B. Qua B vẽ một cát tuyến cắt các đường tròn (O) và (O’) lần lượt tại C và D.

a) CMR : AC = AD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

b, Tìm quỹ tích trung điểm M của CD khi cát tuyến CBD quay quanh B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Cho (O) đường kính AB; C chạy trên một nửa đường tròn. Vẽ đường tròn tâm I tiếp xúc với đường tròn (O) tại C, tiếp xúc với đường kính AB tại D. Đường tròn này cắt CA, CB lần lượt tại M và N.

a) CMR: 3 điểm M, I, N thẳng hàng .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

b, CMR:ID vuông góc với MN .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

c, CMR: đường thẳng CD đi qua một điểm cố định.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

d, Suy ra cách dựng đường tròn (I) nói trên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Cho đường tròn (O) ngoại tiếp tam giác ABC, từ điểm M trên cung BC không chứa điểm A, hạ các đường vuông góc với BC; CA; AB lần lượt tại D; H; K. Chứng minh rằng: $\frac{B C}{M D} = \frac{C A}{M H} + \frac{A B}{M K}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Hai đường tròn (O) và (O’) cắt nhau tại A và B. Các điểm M và N theo thứ tự di chuyển trên các đường tròn (O) và (O’) sao cho chiều từ A đến M và từ A đến N trên các đường tròn (O) và (O’) đều theo chiều quay của kim đồng hồ và các cung AM và AN có số đo bằng nhau. Chứng minh rằng đường trung trực của MN luôn đi qua một điểm cố định.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Bright

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý