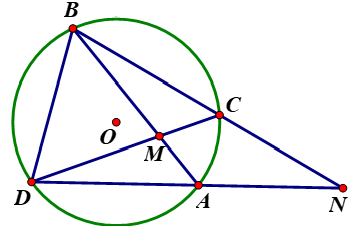
Dạng 3: Góc có đỉnh bên trong và bên ngoài đường tròn có đáp án

34 người thi tuần này 4.6 1.9 K lượt thi 18 câu hỏi 50 phút

Câu 1

Cho tứ giác ABCD có bốn đỉnh thuộc đường tròn . Gọi M, N, P, Q lần lượt là điểm chính giữa các cung AB, BC, CD, DA. Chứng minh rằng : . $M P ⊥ N Q$

Xem đáp án

Lời giải

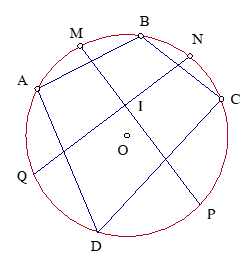
Cho tứ giác ABCD có bốn đỉnh thuộc đường tròn . Gọi M, N, P, Q lần lượt là điểm chính giữa các cung AB, BC, CD, DA. (ảnh 1)

Gọi I là giao điểm của MP và NQ. Ta có.

$\hat{M I Q}$ = $\frac{1}{2}$ (sđ $\overset{⏜}{M Q}$ + sđ $\overset{⏜}{N P}$ )

= $\frac{1}{2}$ . $\frac{1}{2}$ (sđ $\overset{⏜}{A B}$ + sđ $\overset{⏜}{A D}$ + sđ $\overset{⏜}{B C}$ + sđ $\overset{⏜}{C D}$ ).

= $\frac{1}{4} . 360^{o} = 90^{o}$ . Vậy MP ^ NQ.

Câu 2

Cho đường tròn (O), hai đường kính AB và CD vuông góc với nhau, điểm M thuộc cung nhỏ BC. Gọi E là giao điểm của MA và CD, F là giao điểm của MD và AB. Chứng minh rằng:

a) $\hat{DAE} = \hat{A F D}$

Xem đáp án

Lời giải

Cho đường tròn (O), hai đường kính AB và CD vuông góc với nhau, điểm M thuộc cung nhỏ BC. (ảnh 1)

$\hat{DAE} = \frac{sd \overset{⏜}{DBM}}{2}$ (góc nội tiếp) .

$\hat{AFD} = \frac{sd \overset{⏜}{DB} + s d \overset{⏜}{M B}}{2} = \frac{sd \overset{⏜}{DBM}}{2}$ ( góc có đỉnh ở bên trong đường tròn)

Suy ra $\hat{DAE} = \hat{A F D}$

Câu 3

b) Khi M di động trên cung nhỏ BC thì diện tích tứ giác AEFD không đổi.

Xem đáp án

Lời giải

b) Ta có: $\hat{D_{1}} = \hat{A_{1}} (= 45^{°})$ và $\hat{E_{1}} = \hat{ADF}$ ( cách chứn minh tương tự câu a) nên $Δ D A E ∽ Δ A D F (g . g)$ Þ $\Rightarrow \frac{D E}{A D} = \frac{A D}{A F} \Rightarrow A F . D E = A D^{2}$ .

Mặt khác AEFD là tứ giác có hai đường chéo AF, DE vuông góc với nhau.

Do đó $S_{A E F D} = \frac{1}{2} AF \cdot DE = \frac{1}{2} {AD}^{2}$ , không đổi.

Câu 4

Cho hình vẽ, hãy điền dấu (x) vào ô thích hợp trong bảng sau:

TT

Khẳng định

Đúng

Sai

1
$\hat{A} = \hat{B M D}$

2
$\hat{B M C} = \frac{s đ \overset{⏜}{B C} + s đ \overset{⏜}{A D}}{2}$

3

$\hat{A B N} + \hat{N} = \frac{1}{2} s đ \overset{⏜}{B D}$

4
$\hat{N} = \frac{1}{2} (s đ \overset{⏜}{B D} - s đ \overset{⏜}{A C)}$

Xem đáp án

Lời giải

1. sai 2. đúng 3. đúng 4. đúng

Câu 5

Cho đường tròn (O) trong đó có ba dây bằng nhau AB, AC, BD sao cho hai dây AC, BD cắt nhau tại M tạo thành góc vuông AMB. Tính số đo các cung nhỏ AB, CD.

Xem đáp án

Lời giải

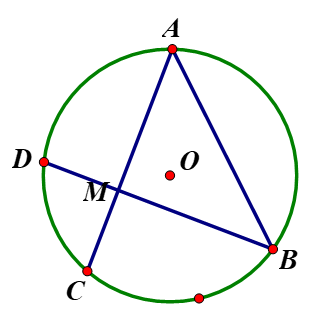
Cho đường tròn (O) trong đó có ba dây bằng nhau AB, AC, BD sao cho hai dây AC, BD cắt nhau tại (ảnh 1)

Đường tròn (O) có dây: AB = AC = BD

Suy ra sđ $\overset{⏜}{A B}$ = sđ $\overset{⏜}{A C}$ = sđ $\overset{⏜}{B D}$

Do đó: sđ $\overset{⏜}{A D}$ = sđ $\overset{⏜}{A C}$ - sđ $\overset{⏜}{C D}$

= sđ $\overset{⏜}{B D}$ - sđ $\overset{⏜}{D C}$ = sđ $\overset{⏜}{B C}$

Theo định lý góc có đỉnh bên trong đường tròn, ta có:

sđ $\overset{⏜}{A D}$ + sđ $\overset{⏜}{B C}$ = 2. sđ $\hat{B M C} = {2.90}^{0} = 180^{0}$

nên sđ

\overset{⏜}{A D}

= sđ

\overset{⏜}{B C}

= 90⁰

Lại có: sđ $\overset{⏜}{A B}$ + sđ $\overset{⏜}{C D}$ = 2. sđ $\hat{A B C} = 180^{0}$

Hơn nữa sđ $\overset{⏜}{A B}$ = sđ $\overset{⏜}{B D}$ = sđ $\overset{⏜}{B C}$ + sđ $\overset{⏜}{D C}$ = 90⁰ + sđ $\overset{⏜}{D C}$

Suy ra: sđ

\overset{⏜}{D C}

= 45⁰; sđ

\overset{⏜}{A B}

= 90⁰ + 45⁰ = 135⁰

Câu 6