Quảng cáo
Trả lời:
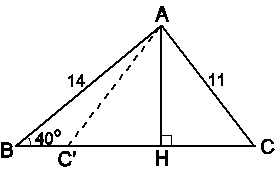
* Tìm cách giải
Vẽ đường cao AH để vận dụng các hệ thức về cạnh và góc trong tam giác vuông. Tính HB và HC từ đó tính được BC.
* Trình bày lời giải
Vẽ đường cao AH. Xét DABH vuông tại H có:
(cm).
(cm).
Xét DAHC vuông tại H có: (cm).
· Nếu H nằm giữa B và C thì (cm).
· Nếu C' nằm giữa B và H thì (cm).
Lưu ý: Học sinh có thể chỉ giải một nghiệm hình là chưa đủ. Bài toán có 2 nghiệm hình
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
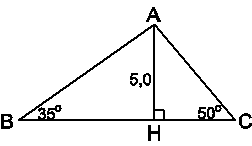
Ta phải tìm AB, AC và BC.
· Xét DABH vuông tại H ta có:
(cm).
· Xét DACH vuông tại H ta có
(cm).
Do đó (cm).
Vậy ; AB = 8,7cm; AC = 6,5cm và BC = 11,3cm.
Lưu ý: Sau khi tính được AB và AC, có thể tính BH và CH theo AB và AC:
Tuy nhiên, ta nên tính BH và CH theo các số đo đã cho trong đề bài để kết quả được chính xác hơn.
Lời giải
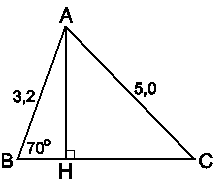
Vẽ đường cao AH. Xét DABH vuông tại H có:
(cm).
(cm).
Xét DAHC vuông tại H có:
(cm).
Điểm C không thể nằm giữa H và B vì trên tia HB có HC > HB. Chỉ còn trường hợp điểm H nằm giữa B và C. Ta có (cm).