Cho tam giác ABC có các góc B và C nhọn, đường cao AH . Dựng ra phía ngoài tam giác ABC các tam giác vuông cân ABD, ACE(). Gọi M là trung điểm của DE. Chứng minh rằng H, A, M thẳng hàng.
Cho tam giác ABC có các góc B và C nhọn, đường cao AH . Dựng ra phía ngoài tam giác ABC các tam giác vuông cân ABD, ACE(). Gọi M là trung điểm của DE. Chứng minh rằng H, A, M thẳng hàng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dựng hình bình hành .
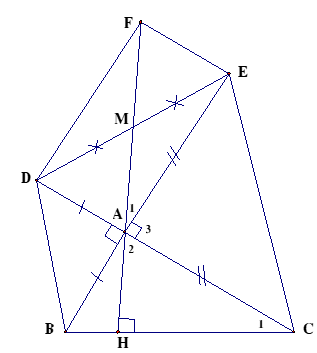
là trung điểm của EF (t/c hình bình hành) và .
Mặt khác (gt); (cùng bù với ).
(c – g – c).
( Hai góc tương ứng).
Mà
.
hay ,A , H thẳng hàng.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
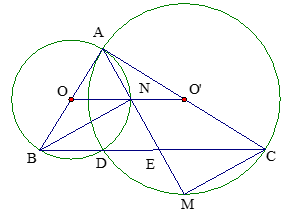
Xét (O’) có: ( góc có đỉnh ở bên trong đường tròn).
( góc tạo bởi tia tiếp tuyến và dây cung) .
Suy ra Þ tam giác ABE cân tại B nên BN vừa là đường cao vừa là trung tuyến Þ NA = NE và OA = OB, O’A = O’C Þ NO, NO’ là đường trung bình của tam giác ACE, ABE nên O’N // CE, NO // EB do đó O, N, O’ thẳng hàng.
Lời giải
a) Tứ giác ADBE là hình thoi vì AM = MB; MD = ME và
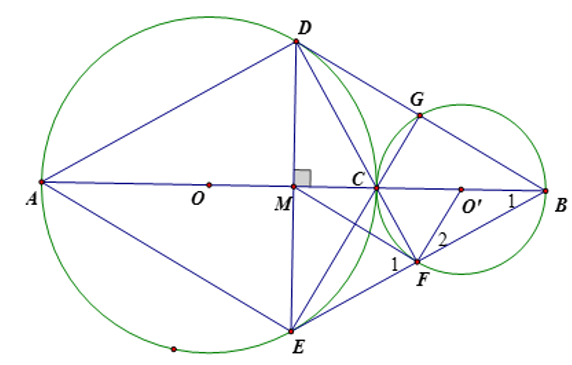
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo