Cho góc và điểm A nằm trong góc đó. Xác định điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho OB = OC và tổng AB +AC là nhỏ nhất .
Cho góc và điểm A nằm trong góc đó. Xác định điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho OB = OC và tổng AB +AC là nhỏ nhất .
Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 7: Cực trị hình học có đáp án !!
Quảng cáo
Trả lời:
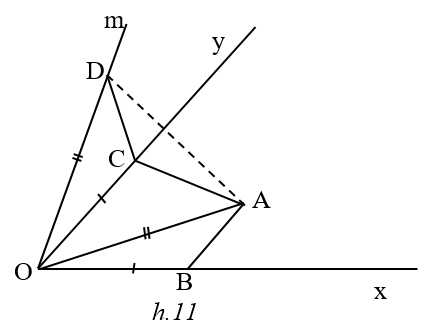
Kẻ tia Om nằm ngoài góc xOy sao cho . Trên tia Om lấy điểm D sao cho OD = OA . Các điểm D và A cố định .
OD =OA, OC = OB ,
Tam giác DOC = tam giác AOB CD = AB
Do đó AC +AB = AC +CD
Mà AC +CD ≥ AD
AC +AB ≥ AD
Xảy ra đẳng thức khi và chỉ khi C thuộc AD
Vậy min(AC+AB) =AD . Khi đó C là giao điểm của AD và Oy, B thuộc tia Ox sao cho OB = OC.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
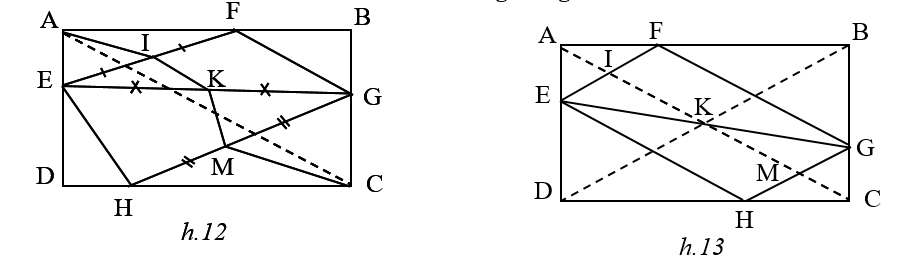
Gọi I ,K, L theo thứ tự là trung điểm của EF, EG , EH (h.12).
tam giác AEF vuông tại A có AI là trung tuyến
Tam giác CGH vuông tại C có CM là trung tuyến
IK là đường trung bình của DEFG
KM là đường trung bình của DEGH
Do đó : chu vi EFGH = EF +FG +GH +EH =2(AI + IK + KM + MC)
Ta lại có : AI + IK + KM + MC ≥ AC
Suy ra chu vi EFGH ≥ 2AC ( độ dài AC không đổi )
Chu vi EFGH nhỏ nhất bằng 2AC Û A,I,K,M,C thẳng hàng.
Khi đó ta có EH//AC,FG//AC, nên EF//DB , tương tự GH//DB . Suy ra tứ giác EFGH là hình bình hành có các cạnh song song với các đường chéo của hình chữ nhật ABCD (h.13).