✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

20/10/2022 2,324

Cho hình vuông ABCD có cạnh bằng 4cm. Trên các cạnh AB, BC,CD,DA, lấy theo thứ tự các điểm E,F,G,H sao cho AE = BF = CG = DH . Tính độ dài AE sao cho tứ giác EFGH có chu vi nhỏ nhất.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 7: Cực trị hình học có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

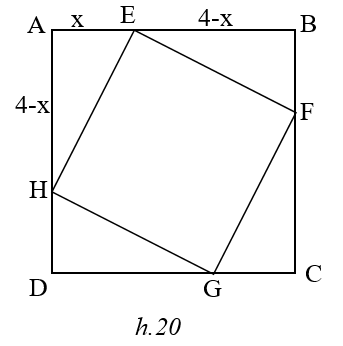
Media VietJack

Tam giác AHE = tam giác BEF = tam giác CFG = tam giác DGH

$\Rightarrow$ HE = EF = FG = GH , HEF = 90⁰

$\Rightarrow$ HEFG là hình vuông nên chu vi EFGH nhỏ nhất khi HE nhỏ nhất .

Đặt AE = x thì HA = EB = 4-x

Tam giác HAE vuông tại A nên :

HE ² = AE² +AE² = x² + (4 - x)² = 2x² - 8x +16 = 2(x - 2)² +8 ≥ 8

HE = $\sqrt{8}$ =2 $\sqrt{2}$ $\Leftrightarrow$ x = 2

Chu vi tứ giác EFGH nhỏ nhất bằng 8 $\sqrt{2}$ cm , khi đó AE = 2 cm .

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác vuông ABC có độ dài các cạnh góc vuông AB = 6 cm, AC = 8cm. M là điểm di chuyển trên cạnh huyền BC. Gọi D và E là chân các đường vuông góc kẻ từ M đến AB và AC . Tính diện tích lớn nhất của tứ giác ADME.

Xem đáp án

Lời giải

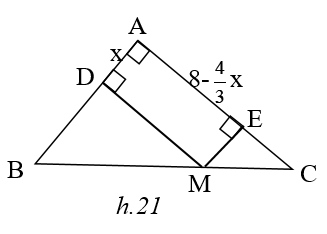
Media VietJack

ADME là hình chữ nhật .

Đặt AD = x thì ME = x

ME //AB

\Rightarrow

\frac{E M}{A B} = \frac{C E}{C A} \Rightarrow \frac{x}{6} = \frac{C E}{8} \Rightarrow C E = \frac{4}{3} x

$\Rightarrow$ AE = 8 - $\frac{4}{3}$ x

Ta có : S_ADME = AD .AE = x ( 8 - $\frac{4}{3}$ x ) = 8x - $\frac{4}{3}$ x² = - $\frac{4}{3}$ (x - 3)² +12 ≤ 12

S_ADME = 12 cm² $\Leftrightarrow$ x =3

Diện tích lớn nhất của tứ giác ADME bằng 12 cm² ,khi đó D là trung điểm của AB , M là trung điểm của BC và E là trung điểm của AC.

Xem thêm các câu hỏi khác »