Cho tam giác vuông ABC có độ dài các cạnh góc vuông AB = 6 cm, AC = 8cm. M là điểm di chuyển trên cạnh huyền BC. Gọi D và E là chân các đường vuông góc kẻ từ M đến AB và AC . Tính diện tích lớn nhất của tứ giác ADME.
Cho tam giác vuông ABC có độ dài các cạnh góc vuông AB = 6 cm, AC = 8cm. M là điểm di chuyển trên cạnh huyền BC. Gọi D và E là chân các đường vuông góc kẻ từ M đến AB và AC . Tính diện tích lớn nhất của tứ giác ADME.
Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 7: Cực trị hình học có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
ADME là hình chữ nhật .
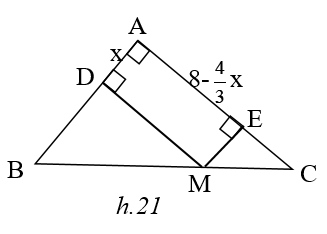
Đặt AD = x thì ME = x
ME //ABAE = 8 -x
Ta có : SADME = AD .AE = x ( 8 - x ) = 8x - x2 = -(x - 3)2 +12 ≤ 12
SADME = 12 cm2 x =3
Diện tích lớn nhất của tứ giác ADME bằng 12 cm2 ,khi đó D là trung điểm của AB , M là trung điểm của BC và E là trung điểm của AC.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
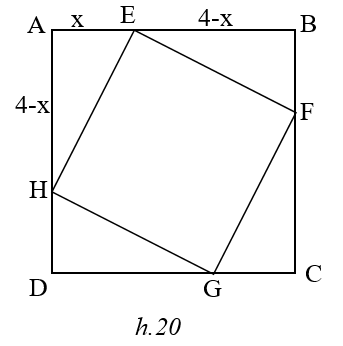
Tam giác AHE = tam giác BEF = tam giác CFG = tam giác DGH
HE = EF = FG = GH , HEF = 900
HEFG là hình vuông nên chu vi EFGH nhỏ nhất khi HE nhỏ nhất .
Đặt AE = x thì HA = EB = 4-x
Tam giác HAE vuông tại A nên :
HE 2 = AE2 +AE2 = x2 + (4 - x)2 = 2x2 - 8x +16 = 2(x - 2)2 +8 ≥ 8
HE = =2 x = 2
Chu vi tứ giác EFGH nhỏ nhất bằng 8 cm , khi đó AE = 2 cm .
Nhắn tin Zalo