Cho tam giác ABC và điểm M thuộc cạnh BC thoả mãn ∆AMB = ∆AMC (Hình 21). Chứng minh rằng:
M là trung điểm của đoạn thẳng BC
Cho tam giác ABC và điểm M thuộc cạnh BC thoả mãn ∆AMB = ∆AMC (Hình 21). Chứng minh rằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì ∆AMB = ∆AMC nên: MB = MC (hai cạnh tương ứng);
\(\widehat {BAM}\) = \(\widehat {CAM}\), \(\widehat {AMB}\) = \(\widehat {AMC}\) (hai góc tương ứng)
Do điểm M nằm giữa hai điểm B, C và MB = MC nên M là trung điểm của đoạn thẳng BC.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Vì ∆ABC = ∆MNP nên \(\widehat A\) = \(\widehat M\)( hai góc tương ứng)
Do \(\widehat A\) + \(\widehat N\) = \(\widehat M\) + \(\widehat N\) Mà \(\widehat A\) + \(\widehat N\) = 125o nên \(\widehat M\) + \(\widehat N\) = 125o.
Ta có \(\widehat M\) + \(\widehat N\) + \(\widehat P\) = 180o (tổng ba góc của một tam giác)
Suy ra 125o + \(\widehat P\) = 180o vì thế \(\widehat P\) = 180o – 125o = 55o.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
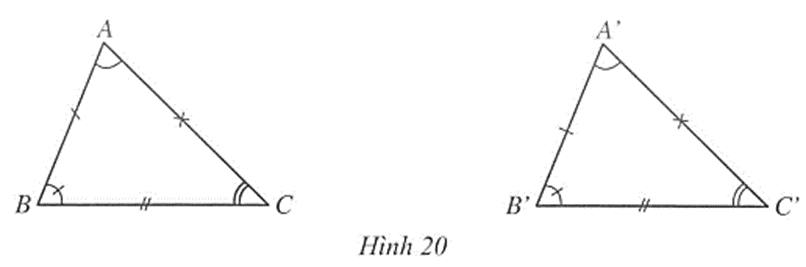
- Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
- Khi hai tam giác ABC và A’B’C’ bằng nhau thì ta kí hiệu là: ∆ABC = ∆A’B’C’.
+ Nếu AB = A’B’, BC = B’C’, CA = C’A’ và \(\widehat A\)= \(\widehat {A'}\), \(\widehat B\)= \(\widehat {B'}\), \(\widehat C\)= \(\widehat {C'}\) thì ∆ABC = ∆A’B’C’.
+ Nếu ∆ABC = ∆A’B’C’ thì AB = A’B’, BC = B’C’, CA = C’A’ và \(\widehat A\)= \(\widehat {A'}\), \(\widehat B\)= \(\widehat {B'}\), \(\widehat C\)= \(\widehat {C'}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập