Cho tam giác ABC có AB = \(\sqrt {15} \) cm và AC = 2BC. Tìm độ dài hai cạnh AC, BC sao cho ABC là một tam giác vuông.

Lời giải

a)

Tam giác FBD và tam giác CED cùng vuông tại D có:

\(\widehat F = \widehat C\,\,\,\,\,\left( { = 90^\circ - \widehat B} \right)\).

Do đó, ∆BDF ᔕ ∆EDC (góc nhọn).

b)

Tam giác ABC vuông tại A và tam giác DEC vuông tại D có:

\(\widehat C\) chung

Do đó, ∆ABC ᔕ ∆DEC (góc nhọn). Suy ra \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DC}}\).

Vì AD là phân giác của góc BAC trong tam giác ABC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\).

Suy ra \(\frac{{AC}}{{DC}} = \frac{{AB}}{{BD}}\).

Do đó \(\frac{{AB}}{{DE}} = \frac{{AB}}{{BD}}\). Suy ra BD = DE.

Lời giải

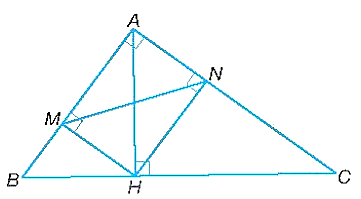
a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 3² + 4² = 25 nên BC = 5 cm.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

\(\widehat C\) chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên \(CH = \frac{{C{A^2}}}{{CB}} = \frac{{{4^2}}}{5} = \frac{{16}}{5}\) (cm).

Do đó, BH = BC – CH = 5 – \(\frac{{16}}{5}\) = \(\frac{9}{5}\) (cm).

Vì ∆ABC ᔕ ∆HAC (cmt) nên \(\frac{{AB}}{{HA}} = \frac{{BC}}{{AC}}\)

Do đó, \[AH = \frac{{AB \cdot AC}}{{BC}} = \frac{{3 \cdot 4}}{5} = \frac{{12}}{5}\] (cm).

b)

Vì HM vuông góc AB, suy ra \(\widehat {HMA} = 90^\circ \).

HN vuông góc với AC, suy ra \(\widehat {HNA} = 90^\circ \).

Tứ giác ANHM có: \(\widehat {HMA} = \widehat {NAM} = \widehat {HNA} = 90^\circ \) nên tứ giác ANHM là hình chữ nhật.

Do đó, \(\widehat {NHM} = 90^\circ \).

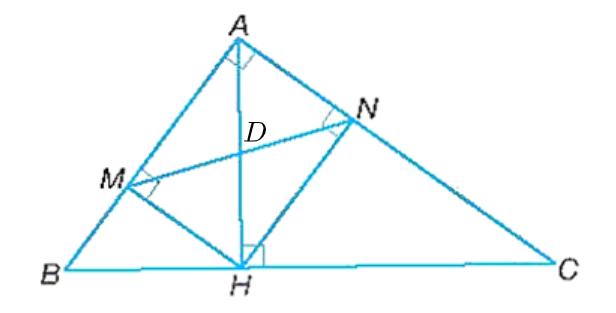
Gọi D là giao điểm của hai đường chéo trong hình chữ nhật NHMA nên DH = DM. Do đó, tam giác DHM cân tại D.

Suy ra: \(\widehat {DHM} = \widehat {DMH}\)

Lại có: \(\widehat {DHM} = \widehat B\,\,\,\left( { = 90^\circ - \widehat {MHB}} \right)\) nên \(\widehat {DMH} = \widehat B\).

Xét tam giác HMN vuông tại H và tam giác ABC vuông tại A có:

\(\widehat {NMH} = \widehat B\) (do \(\widehat {DMH} = \widehat B\))

Do đó, ∆HMN ᔕ ∆ABC (góc nhọn).