Chọn phương án đúng.

Cho đường tròn (O; R) và hai đường thẳng a₁ và a₂. Gọi d₁, d₂ lần lượt là khoảng cách từ điểm O đến a₁ và a₂. Biết rằng (O) cắt a₁ và tiếp xúc với a₂ (H.5.44). Khi đó:

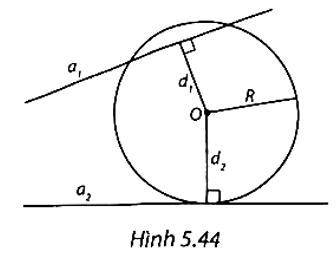
A. d₁ < R và d₂ = R.

B. d₁ = R và d₂ < R.

C. d₁ > R và d₂ = R.

D. d₁ < R và d₂ < R.

(H.5.51)

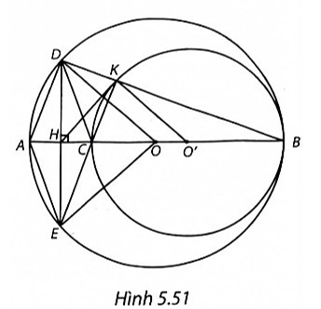
a) Gọi R, r lần lượt là bán kính của hai đường tròn (O) và (O').

Ta có OO' = R – r nên hai đường tròn (O) và (O') tiếp xúc trong với nhau.

b) Tam giác ODE cân tại O (OD = OE = R) có OH là đường cao nên đồng thời là đường trung tuyến của ∆ODE, hay DH = HE.

Tứ giác ADCE có hai đường chéo AC và DE cắt nhau tại H là trung điểm mỗi đường nên ADCE là hình bình hành. Lại có AC ⊥ DE tại H, suy ra ADCE là hình thoi.

c) Tam giác KCB có đường trung tuyến KO' và KO' = CO' = BO' nên tam giác KCB là tam giác vuông tại K, suy ra \(\widehat {CKB} = 90^\circ \) hay KC ⊥ KB. (1)

Tương tự, ta có \(\widehat {ADB} = 90^\circ \) hay DA ⊥ DB. (2)

Từ (1) và (2) suy ra KC // AD.

Lại có EC // AD (vì ADCE là hình thoi), do đó ba điểm E, C, K thẳng hàng.

d) Xét tam giác DEK vuông tại K có KH là đường trung tuyến nên KH = DH = EH.

Do đó tam giác KHE cân tại H, suy ra \(\widehat {HKE} = \widehat {HEK}.\)

Lại có, ∆O'CK cân tại O' nên \(\widehat {O'CK} = \widehat {O'KC}.\)

\(\widehat {HKE} + \widehat {O'CK} = \widehat {HKE} + \widehat {O'KC}\)

\(\widehat {O'KH} = \widehat {HKE} + \widehat {O'CK}.\)

Mặt khác \(\widehat {O'CK} = \widehat {HCE}\) (hai góc đối đỉnh).

Tam giác HEC vuông tại H nên \(\widehat {KEH} + \widehat {HCE} = 90^\circ .\)

Suy ra \(\widehat {HKE} + \widehat {O'CK} = \widehat {HKE} + \widehat {HCE}\)  \( = \widehat {KEH} + \widehat {HCE} = 90^\circ \) hay \(\widehat {O'KH} = 90^\circ .\)

Do đó HK ⊥ O'K.

Vậy HK là tiếp tuyến của đường tròn (O').

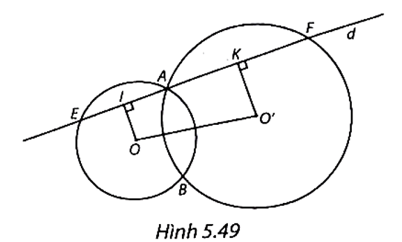
(H.5.50)

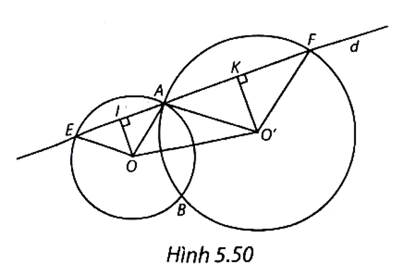
a) ∆AOE là tam giác cân tại O (OA = OE) có OI là đường trung tuyến (vì I là trung điểm của AE) nên OI cũng là đường cao, tức là \(\widehat {AIO} = 90^\circ \) hay OI ⊥ AI.

Tương tự, đối với tam giác AO'F, ta có \(\widehat {AKO'} = 90^\circ \) hay O'K ⊥ KF.

Do đó OI // O'K (cùng vuông góc với d).

Tứ giác OO'KI có OI // O'K và \(\widehat {OIK} = \widehat {O'KI} = 90^\circ \) nên OO'KI là hình thang vuông.

b) Theo đề bài, EI = IA và AK = KF nên ta có EA = 2IA và AF = 2AK.

Ta có: EF = EA + AF = 2IA + 2AK = 2(IA + AK) = 2IK. Do đó \(IK = \frac{1}{2}EF.\)

c) Khi d đi qua A thì tứ giác OO'KI luôn là hình thang vuông.

Nếu hình thang vuông đó là hình chữ nhật thì IK // OO', hay d // OO'.

Ngược lại, nếu d // OO' thì IK // OO' nên OO'KI là hình chữ nhật.

Vậy để tứ giác OO'KI là hình chữ nhật thì d // OO'.