Cùng một lúc Hùng đi từ A đến B, còn Dũng đi từ B đến A. Hai bạn gặp nhau lần đầu ở điểm C cách A 3km, rồi lại tiếp tục đi. Hùng đi đến B rồi quay lại A ngay, còn Dũng đi đến A rồi quay lại B ngay. Hai bạn gặp nhau một lần nữa ở điểm D cách B 2km. Tính quãng đường AB và cho biết ai đi nhanh hơn?
Cùng một lúc Hùng đi từ A đến B, còn Dũng đi từ B đến A. Hai bạn gặp nhau lần đầu ở điểm C cách A 3km, rồi lại tiếp tục đi. Hùng đi đến B rồi quay lại A ngay, còn Dũng đi đến A rồi quay lại B ngay. Hai bạn gặp nhau một lần nữa ở điểm D cách B 2km. Tính quãng đường AB và cho biết ai đi nhanh hơn?
Câu hỏi trong đề: 17 bài tập Bài toán tỉ lệ thuận có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có sơ đồ:
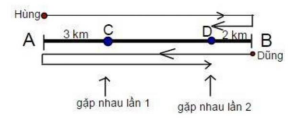
Khi Hùng gặp Dũng gặp nhau lần thứ nhất ở C thì cả 2 bạn đã đi được vừa đúng một lần quãng đường AB, trong đó Hùng đi được 3km.
Đến khi gặp nhau lần thứ hai ở D thì cả hai bạn đã đi được vừa đúng 3 lần quãng đường AB, trong đó Hùng đã đi được:
\(3 \times 3 = 9\) (km)
Vì \(9km = AB + 2km\) nên \(AB = 9 - 2 = 7\) (km)
Khi gặp nhau lần đầu Hùng đi được 3km còn Dũng đi được:
\(7 - 3 = 4\) (km)
Vậy Dũng đi nhanh hơn Hùng.
Đáp Số: AB = 7m; Dũng đi nhanh hơn Hùng.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đổi 1 tá = 12 chiếc.
Lập bảng:
|
|
Số chiếc khăn |
Khối lượng sợi |
|
Giá trị thứ nhất |
12 |
530 |
|
Giá trị thứ hai |
78 |
?? |
Số gam sợi cần để dệt 78 chiếc khăn là:
\(\frac{{78 \times 530}}{{12}} = 3445\) (g)
Đáp Số: 3 445g
Lời giải
Trước hết ta đưa bài toán về dạng có 3 đại lượng như sau:
Số giờ làm của 3 ngày, mỗi ngày làm 8 giờ là: 3 × 8 = 24 (giờ)
Số giờ làm của 5 ngày, mỗi ngày làm 10 giờ là: 4 × 10 = 40 (giờ)
Từ đó ta đưa bài toán về dạng có 3 đại lượng được tóm tắt như sau:
5 công nhân ---- 24 giờ --- 30 m³
7 công nhân ---- 40 giờ ---- x m³
Ta thấy:
- Số công nhân tỉ lệ thuận với số m³ đất đào được.
- Số giờ làm tỉ lệ thuận với số m³ đất đào được.
Đây là bài toán tỉ lệ thuận kép nên ta chia bài toán thành hai bài toán nhỏ như sau:
Bài Toán 1: Giữ nguyên số giờ làm là 24 giờ ta tính xem 7 công nhân đào được bao nhiêu m³?
|
|
Số công nhân |
Số m3 đất |
|
Giá trị thứ nhất |
5 |
30 |
|
Giá trị thứ hai |
7 |
y =? |
7 công nhân đào trong 24 giờ được số m³ đất là:
\(\frac{{7 \times 30}}{5} = 42({m^3})\)
Bài Toán 2: Giữ nguyên số công nhân là 7 người xem trong 40 giờ họ đào được bao nhiêu m³ đất:
|
|
Số giờ làm việc |
Số m3 đất |
|
Giá trị thứ nhất |
24 |
42 |
|
Giá trị thứ hai |
40 |
x = ? |
7 công nhân đào trong 40 giờ được số m³ đất là:
\(\frac{{40 \times 42}}{{24}} = 70({m^3})\)
Học sinh trình bày lời giải như sau:
Số giờ làm của 3 ngày, mỗi ngày làm 8 giờ là: 3 × 8 = 24 (giờ)
Số giờ làm của 5 ngày, mỗi ngày làm 10 giờ là: 4 × 10 = 40 (giờ)
7 công nhân đào trong 24 giờ được số m³ đất là: \(\frac{{7 \times 30}}{5} = 42({m^3})\)
7 công nhân đào trong 40 giờ được số m³ đất là: \(\frac{{40 \times 42}}{{24}} = 70({m^3})\)
Đáp Số: 70 m³
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập