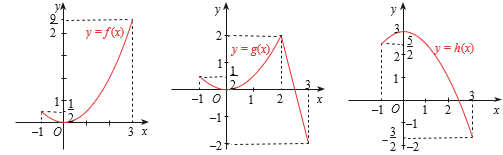
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
y = f (x) = 2x + 3 trên đoạn [−3; 1];
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: y = f (x) = 2x + 3 trên đoạn [−3; 1] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid0-1753948971.png)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
y = f (x) = 2x + 3 trên đoạn [−3; 1];
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét hàm số \(f(x) = 2x + 3\) trên đoạn \([ - 3;1]\).
Với mọi \(x \in [ - 3;1]\), ta có \(f(x) = 2x + 3 \ge - 3\). Mặt khác \(f( - 3) = - 3\). Do đó \({\min _{[ - 3;1]}}f(x) = - 3\).
Với mọi \(x \in [ - 3;1]\), ta có \(f(x) = 2x + 3 \le 5\). Mặt khác \(f(1) = 5\). Do đó \({\max _{[ - 3;1]}}f(x) = 5\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Các hàm số đạt giá trị lớn nhất hoặc giá trị nhỏ nhất trên đoạn [–1; 3] tại điểm đầu mút của đoạn hoặc tại điểm cực trị trong khoảng (–1; 3).
Lời giải
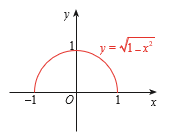
Xét hàm số \(g(x) = \sqrt {1 - {x^2}} \).
Tập xác định: \(D = [ - 1;1]\).
Ta có \(0 \le g(x) \le 1\) với mọi \(x \in [ - 1;1]\). Mặt khác \(g(0) = 1\) và \(g(1) = 0\).
Do đó \({\min _{[ - 1;1]}}g(x) = 0\) và \({\max _{[ - 1;1]}}g(x) = 1\).
Nhắn tin Zalo