Hình vẽ dưới đây cho ta đồ thị của ba hàm số
f (x) = \[\frac{1}{2}{x^2}\]; g(x) = \[\left\{ \begin{array}{l}\frac{1}{2}{x^2}{\rm{ , x}} \le {\rm{2}}\\ - 4x + 10{\rm{ , x}} \ge {\rm{2}}\end{array} \right.\] và h(x) = \[3 - \frac{1}{2}{x^2}\] trên đoạn [−1; 3].
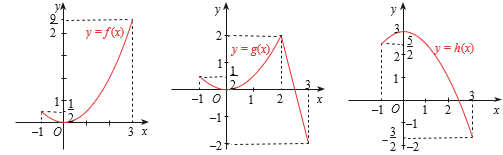
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: y = f (x) = 2x + 3 trên đoạn [−3; 1] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid0-1753948971.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Xét hàm số \(f(x) = 2x + 3\) trên đoạn \([ - 3;1]\).
Với mọi \(x \in [ - 3;1]\), ta có \(f(x) = 2x + 3 \ge - 3\). Mặt khác \(f( - 3) = - 3\). Do đó \({\min _{[ - 3;1]}}f(x) = - 3\).
Với mọi \(x \in [ - 3;1]\), ta có \(f(x) = 2x + 3 \le 5\). Mặt khác \(f(1) = 5\). Do đó \({\max _{[ - 3;1]}}f(x) = 5\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
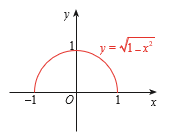
Xét hàm số \(g(x) = \sqrt {1 - {x^2}} \).
Tập xác định: \(D = [ - 1;1]\).
Ta có \(0 \le g(x) \le 1\) với mọi \(x \in [ - 1;1]\). Mặt khác \(g(0) = 1\) và \(g(1) = 0\).
Do đó \({\min _{[ - 1;1]}}g(x) = 0\) và \({\max _{[ - 1;1]}}g(x) = 1\).
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập