Hai đơn vị bộ đội đóng quân ở hai vị trí A và B cách nhau 9km được lệnh xuất phát lúc 8 giờ tối đến hợp quân ở C để cùng thi hành một nhiệm vụ. Cả hai đơn vị đi trên cùng một con đường theo cùng một chiều đến C.
Đơn vị xuất phát từ A hành quân với vận tốc 6 km/giờ.
Đơn vị xuất phát từ B hành quân với vận tốc 4,5 km/giờ.
Để giữ bí mật, hai đơn vị không liên lạc với nhau bằng vô tuyến điện mà dùng một con chim bồ câu đưa thư bay qua bay lại với vận tốc 28km/giờ để truyền tin. Chim bồ câu bay cho đến khi hai đơn vị hội quân.
Tính quãng đường chim bay?
Hai đơn vị bộ đội đóng quân ở hai vị trí A và B cách nhau 9km được lệnh xuất phát lúc 8 giờ tối đến hợp quân ở C để cùng thi hành một nhiệm vụ. Cả hai đơn vị đi trên cùng một con đường theo cùng một chiều đến C.
Đơn vị xuất phát từ A hành quân với vận tốc 6 km/giờ.
Đơn vị xuất phát từ B hành quân với vận tốc 4,5 km/giờ.
Để giữ bí mật, hai đơn vị không liên lạc với nhau bằng vô tuyến điện mà dùng một con chim bồ câu đưa thư bay qua bay lại với vận tốc 28km/giờ để truyền tin. Chim bồ câu bay cho đến khi hai đơn vị hội quân.
Tính quãng đường chim bay?
Câu hỏi trong đề: 13 bài tập Các dạng toán chuyển động khác có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thời gian bồ câu bay qua bay lại đúng bằng thời gian đơn vị thứ nhất hành quân để đuổi kịp đơn vị thứ hai. Thời gian đó là:
\(9:(6 - 4,5) = 6\) (giờ)
Quãng đường chim đã bay qua bay lại tất cả là:
\(28 \times 6 = 168\) (km)
Đáp Số: 168 km.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
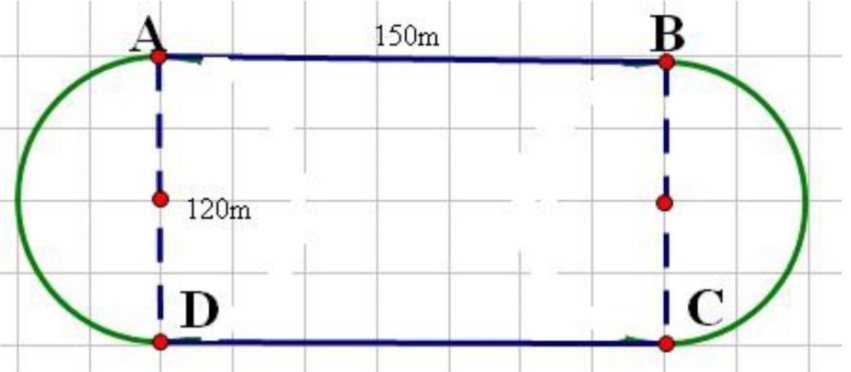
Mỗi nửa đường tròn dài: \(120 \times 3,14:2\) (mét)
Vậy hai nửa đường tròn dài: \(120 \times 3,14 = 376,8\) (m)
Cả đường chạy dài: \(376,8 + 150 \times 2 = 676,8\) (m)
Tổng vận tốc hai người chạy là: \(676,8:28,2 = 24\) (m/giây)
Hiệu vận tốc hai người là: \(676,8:338,4 = 2\) (m/giây)
Vận tốc của người chạy nhanh là: \((24 + 2):2 = 13\) (m/giây)
Vận tốc của người chạy chậm là: \(13 - 2 = 11\) (m/giây)
Đáp Số: 11 m/giây và 13 m/giây.
Lời giải
Khi gặp nhau lần thứ hai thì tổng quãng đường hai người đi được bằng 3 lần quãng đường AB. Hai người gặp nhau lần đầu tại C cách A 4 km hay nói cách khác khi đó người thứ nhất đã đi được 4 km. Vậy cứ mỗi lần hai người đi được tổng quảng đường là AB thì người thứ nhất đi được 4 km. Vậy:
Đến khi gặp nhau lần 2 thì người thứ nhất đi được: \(3 \times 4 = 12\) km.
Quãng đường người thứ nhất đi được bằng quãng đường AB cộng thêm 3 km.
Quãng đường AB là: \(12 - 3 = 9\) km.
Đáp Số: 9 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập