Bạn An xuất phát từ A, cứ tiến 10 bước rồi lùi 2 bước, lại tiến 10 bước rồi lùi 1 bước, xong lại tiến 10 bước rồi lùi 2 bước, lại tiến 10 bước rồi lùi 1 bước, rồi cứ tiếp tục theo quy luật như vậy cho đến khi dừng lại ở B. Lúc đến B bạn An đếm thấy mình đã thực hiện đúng 471 bước. Hỏi B cách A bao nhiêu bước chân của An?
Bạn An xuất phát từ A, cứ tiến 10 bước rồi lùi 2 bước, lại tiến 10 bước rồi lùi 1 bước, xong lại tiến 10 bước rồi lùi 2 bước, lại tiến 10 bước rồi lùi 1 bước, rồi cứ tiếp tục theo quy luật như vậy cho đến khi dừng lại ở B. Lúc đến B bạn An đếm thấy mình đã thực hiện đúng 471 bước. Hỏi B cách A bao nhiêu bước chân của An?
Câu hỏi trong đề: 13 bài tập Các dạng toán chuyển động khác có lời giải !!
Quảng cáo
Trả lời:
Cách bước là: \(10 - 2 + 10 - 1 + 10 - 2 + 10 - 1....\)
Mỗi Chu kì phải bước: \(10 + 2 + 10 + 1 = 23\) bước
Mỗi chu kì tiến được: \(10 - 2 + 10 - 1 = 17\) bước
Số chu kì: \(471:23 = 20\) chu kì dư 11 bước
Dư 11 bước theo chu kì chỉ tiến 10 lùi có 1 là được 9 bước
A cách B: \(17 \times 20 + 9 = 349\) bước.
Đáp Số: 349 bước.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
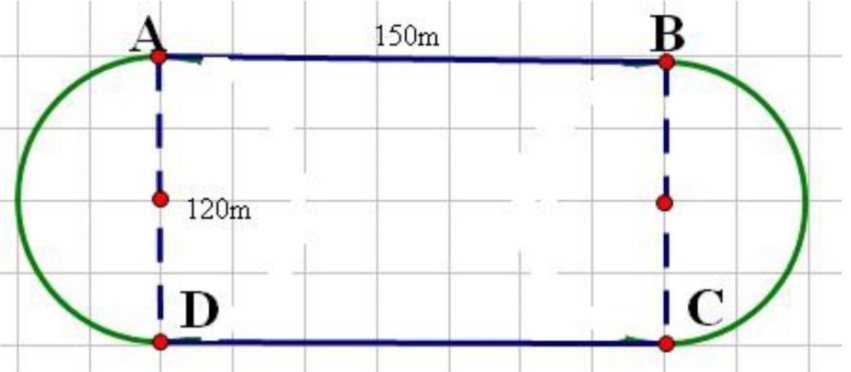
Mỗi nửa đường tròn dài: \(120 \times 3,14:2\) (mét)
Vậy hai nửa đường tròn dài: \(120 \times 3,14 = 376,8\) (m)
Cả đường chạy dài: \(376,8 + 150 \times 2 = 676,8\) (m)
Tổng vận tốc hai người chạy là: \(676,8:28,2 = 24\) (m/giây)
Hiệu vận tốc hai người là: \(676,8:338,4 = 2\) (m/giây)
Vận tốc của người chạy nhanh là: \((24 + 2):2 = 13\) (m/giây)
Vận tốc của người chạy chậm là: \(13 - 2 = 11\) (m/giây)
Đáp Số: 11 m/giây và 13 m/giây.
Lời giải
Thời gian bồ câu bay qua bay lại đúng bằng thời gian đơn vị thứ nhất hành quân để đuổi kịp đơn vị thứ hai. Thời gian đó là:
\(9:(6 - 4,5) = 6\) (giờ)
Quãng đường chim đã bay qua bay lại tất cả là:
\(28 \times 6 = 168\) (km)
Đáp Số: 168 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.