Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2.000.000 đồng mỗi tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ 100.000 đồng mỗi tháng thì có thêm 2 căn hộ bị bỏ trống. Muốn có thu nhập cao nhất, công ty đó phải cho thuê với giá mỗi căn hộ là bao nhiêu?
Quảng cáo
Trả lời:
Chọn A
Gọi \(x\) là giá thuê thực tế của mỗi căn hộ, (\(x\): đồng; \(x \ge 2000.000\) đồng)
Ta có thể lập luận như sau:
Tăng giá 100.000 đồng thì có 2 căn hộ bị bỏ trống.
Tăng giá \(x - 2.000.000\) đồng thì có bao nhiêu căn hộ bị bỏ trống.
Theo quy tắc tam xuất ta có số căn hộ bị bỏ trống là: \(\frac{{2\left( {x - 2.000.000} \right)}}{{100.000}} = \frac{{x - 2.000.000}}{{50.000}}\)
Do đó khi cho thuê với giá x đồng thì số căn hộ cho thuê là:
\[50 - \frac{{x - 2.000.000}}{{50.000}} = - \frac{x}{{50.000}} + 90\]
Gọi \(F\left( x \right)\) là hàm lợi nhuận thu được khi cho thuê các căn hộ, (\(F\left( x \right)\): đồng).
Ta có: \[F\left( x \right) = \left( { - \frac{x}{{50.000}} + 90} \right)x = - \frac{1}{{50.000}}{x^2} + 90x\] ( bằng số căn hộ cho thuê nhân với giá cho thuê mỗi căn hộ).
Câu toán trở thành tìm giá trị lớn nhất của \[F\left( x \right) = - \frac{1}{{50.000}}{x^2} + 90x\], \(x \ge 2.000.000\)
\(F'\left( x \right) = - \frac{1}{{25.000}}x + 90\); \(F'\left( x \right) = 0 \Leftrightarrow - \frac{1}{{25.000}}x + 90 = 0 \Leftrightarrow x = 2.250.000\)
Bảng biến thiên:
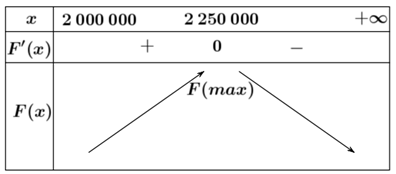
Suy ra \(F\left( x \right)\) đạt giá trị lớn nhất khi \(x = 2.250.000\)
Vậy công ty phải cho thuê với giá 2.250.000 đồng mỗi căn hộ thì được lãi lớn nhất.
Nhận xét:
Sau khi tìm được hàm \[F\left( x \right) = - \frac{1}{{50.000}}{x^2} + 90x\]. Ta không cần phải đi khảo sát và vẽ bảng biến thiên như trên. Đề đã cho bốn đáp án x, ta dùng phím CALC của MTCT để thay lần lượt các giá trị vào, cái nào làm cho \(F\left( x \right)\) lớn nhất chính là giá trị cần tìm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Rộng \(\frac{{\sqrt {34} - 3\sqrt 2 }}{{16}}d\), dài \(\frac{{\sqrt {7 - \sqrt {17} } }}{4}d\)
B. Rộng \(\frac{{\sqrt {34} - 3\sqrt 2 }}{{15}}d\), dài \(\frac{{\sqrt {7 - \sqrt {17} } }}{4}d\)
C. Rộng \(\frac{{\sqrt {34} - 3\sqrt 2 }}{{14}}d\), dài \(\frac{{\sqrt {7 - \sqrt {17} } }}{4}d\)
Lời giải
Chọn A
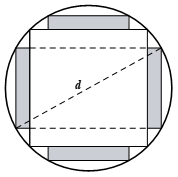
Gọi chiều dài và chiều rộng của miếng phụ lần lượt là x, y. Đường kính của khúc gỗ là d, khi đó tiết diện ngang của thanh xà có độ dài cạnh là \(\frac{d}{{\sqrt 2 }}\) và \(0 < x < \frac{{d\left( {2 - \sqrt 2 } \right)}}{4},0 < y < \frac{d}{{\sqrt 2 }}\)
Theo đề Câu ta được hình chữ nhật ABCD như hình vẽ, theo định lý Pitago ta có:
\({\left( {2x + \frac{d}{{\sqrt 2 }}} \right)^2} + {y^2} = {d^2} \Leftrightarrow y = \frac{1}{{\sqrt 2 }}\sqrt {{d^2} - 8{x^2} - 4\sqrt 2 x} \)
Do đó, miếng phụ có diện tích là: \(S\left( x \right) = \frac{1}{{\sqrt 2 }}\sqrt {{d^2} - 8{x^2} - 4\sqrt 2 dx} \) với \(0 < x < \frac{{d\left( {2 - \sqrt 2 } \right)}}{4}\)
Bài toán trở thành tìm \(x\) để \(S\left( x \right)\) đạt giá trị lớn nhất.
Ta có: \(S'\left( x \right) = \frac{1}{{\sqrt 2 }}\sqrt {{d^2} - 8{x^2} - 4\sqrt 2 dx} + \frac{{x\left( { - 8x - 2\sqrt 2 d} \right)}}{{\sqrt 2 \sqrt {{d^2} - 8{x^2} - 4\sqrt 2 dx} }}\)\( = \frac{{ - 16{x^2} - 6\sqrt 2 dx + {d^2}}}{{\sqrt 2 \sqrt {{d^2} - 8{x^2} - 4\sqrt 2 dx} }}\)
\(S'\left( x \right) = 0 \Leftrightarrow - 16{x^2} - 6\sqrt 2 dx + {d^2} = 0 \Leftrightarrow - 16{\left( {\frac{x}{d}} \right)^2} - 6\sqrt 2 \left( {\frac{x}{d}} \right) + 1 = 0 \Leftrightarrow x = \frac{{\sqrt {34} - 3\sqrt 2 }}{{16}}d\)
Vậy miếng phụ có kích thước \(x = \frac{{\sqrt {34} - 3\sqrt 2 }}{{16}}d,y = \frac{{\sqrt {7 - \sqrt {17} } }}{4}d\)
Câu 2
A. Rộng 6m, dài 12m, cao 8m. Tiền: 216 triệu
B. Rộng 6m, dài 12m, cao 8m. Tiền: 215 triệu
C. Rộng 6m, dài 12m, cao 8m. Tiền: 214 triệu
Lời giải
Chọn A
Gọi \[x,y,h\] lần lượt là chiều dài, chiều rộng, chiều cao của hồ chứa nước, \(\left( {x > 0,y > 0,h > 0,m} \right)\)
Ta có: \(\frac{y}{x} = 2 \Leftrightarrow y = 2x\). Thể tích hồ chứa nước \(V = xyh \Leftrightarrow h = \frac{V}{{xy}} = \frac{{576}}{{x\left( {2x} \right)}} = \frac{{288}}{{{x^2}}}\)
Diện tích cần xây dựng hồ chứa nước:
\(S\left( x \right) = 2xy + 2xh + 2yh = 2x\left( {2x} \right) + 2x\frac{{288}}{{{x^2}}} + 2\left( {2x} \right)\frac{{288}}{{{x^2}}} = 4{x^2} + \frac{{1728}}{x}\)
Để chi phí nhân công là ít nhất thì diện tích cần xây dựng là nhỏ nhất, mà vẫn đạt thể tích như mong muốn.
Bài toán trở thành tìm \(x\) để \(S\left( x \right)\) nhỏ nhất
\( \Leftrightarrow S\left( x \right) = 4{x^2} + \frac{{1728}}{x} \Rightarrow S'\left( x \right) = 0 \Leftrightarrow 8x - \frac{{1728}}{{{x^2}}} = 0 \Leftrightarrow x = 6\)
Bảng biến thiên:
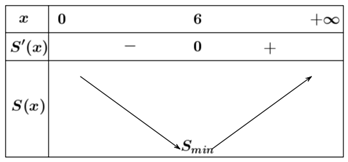
Vậy kích thước của hồ là: rộng 6m, dài 12m, cao 8m.
Diện tích cần xây: \(432{m^2}\) và chi phí ít nhất là: \(432x500.000 = 216.000.000\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Tốc độ bơm giảm từ phút 60 đến phút thứ 90.
B. Tốc độ bơm luôn giảm.
C. Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.