Cho hàm số\(y = \frac{{2x - 1}}{{x + 2}}\). Mệnh đề nào sau đây sai?
Câu hỏi trong đề: Đề kiểm tra Toán 12 Kết nối tri thức Chương 1 có đáp án !!
Quảng cáo
Trả lời:
Chọn D
Hàm số đã cho có:
Tập xác định:\(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Đạo hàm \(y' = \frac{5}{{{{(x + 2)}^2}}} > 0\,,\,\forall x \ne - 2\).
Nên hàm số đồng biến trên từng khoảng xác định của nó và hàm số không có giá trị lớn nhất, giá trị nhỏ nhất.
Tiệm cận đứng \(x = - 2\), tiệm cận ngang \(y = 2\).
Đối chiếu với các phương án ta thấy A đúng, B đúng, C đúng, D sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số \(C = \frac{{19200000}}{{{x^2}}} + \frac{{27x}}{{x + 3000}},\,\,\left( {x \ge 1} \right)\) là chi phí đặt hàng và vận chuyển một linh kiện
Ta có \(C' = - \frac{{38400000}}{{{x^3}}} + \frac{{81000}}{{{{\left( {x + 3000} \right)}^2}}}\).
Cho \(C' = 0 \Leftrightarrow 12800{\left( {x + 3000} \right)^2} - 27{x^3} = 0 \Leftrightarrow x = 2400\).
Lập BBT cho hàm số trên nửa khoảng \(\left[ {1; + \infty } \right)\) ta thu được \({C_{\min }}\) khi \(x = 2400\).
Đáp án: 2400.
Lời giải
Điều kiện \(\left\{ \begin{array}{l}x > 0\\1700 - 7x > 0\end{array} \right. \Leftrightarrow 0 < x < \frac{{1700}}{7}\).
Doanh thu được khi công ty sản xuất và tiêu thụ hết \(x\) sản phẩm là \(R\left( x \right) = xp\left( x \right) = 1700x - 7{x^2}\)
Do đó, lợi nhuận thu được là
\(P\left( x \right) = xp\left( x \right) - C\left( x \right)\)\( = 1700x - 7{x^2} - \left( {16\,000 + 500x - 1,6{x^2} + 0,004{x^3}} \right)\)
\(P\left( x \right) = - 0,004{x^3} - 5,4{x^2} + 1200x - 16\,000\), \(0 < x < \frac{{1700}}{7}\).
\(P'\left( x \right) = - 0,012{x^2} - 10,8x + 1200\); \(P'\left( x \right) = 0 \Leftrightarrow - 0,012{x^2} + 10,8x + 1200 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1000\\x = 100\end{array} \right.\).
Đối chiếu điều kiện ta có \(x = 100\).
Lập bảng biến thiên của hàm số, ta thu được kết quả là \(\mathop {\max }\limits_{\left( {0;\frac{{1700}}{7}} \right)} P\left( x \right) = P\left( {100} \right) = 46\,000\) (triệu).
Vậy công ty cần sản xuất 100 sản phẩm thì lợi nhuận thu được là cao nhất.
Đáp án: 100.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
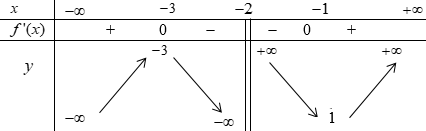
![Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1758958917.png)