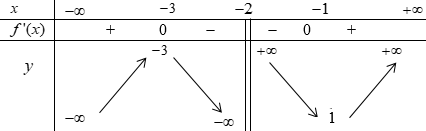
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới?
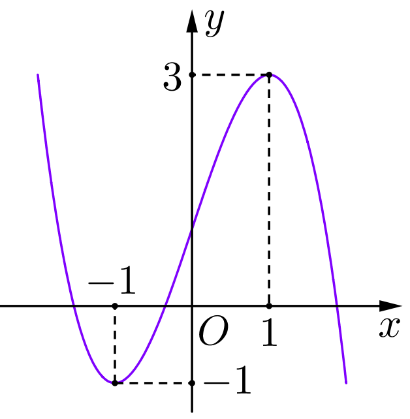
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới?

Câu hỏi trong đề: Đề kiểm tra Toán 12 Kết nối tri thức Chương 1 có đáp án !!
Quảng cáo
Trả lời:
Chọn B
Đồ thị hàm số đi qua điểm \(\left( {1\,;\,3} \right)\) nên hàm số cần tìm là \(y = - {x^3} + 3x + 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số \(C = \frac{{19200000}}{{{x^2}}} + \frac{{27x}}{{x + 3000}},\,\,\left( {x \ge 1} \right)\) là chi phí đặt hàng và vận chuyển một linh kiện
Ta có \(C' = - \frac{{38400000}}{{{x^3}}} + \frac{{81000}}{{{{\left( {x + 3000} \right)}^2}}}\).
Cho \(C' = 0 \Leftrightarrow 12800{\left( {x + 3000} \right)^2} - 27{x^3} = 0 \Leftrightarrow x = 2400\).
Lập BBT cho hàm số trên nửa khoảng \(\left[ {1; + \infty } \right)\) ta thu được \({C_{\min }}\) khi \(x = 2400\).
Đáp án: 2400.
Lời giải
Điều kiện \(\left\{ \begin{array}{l}x > 0\\1700 - 7x > 0\end{array} \right. \Leftrightarrow 0 < x < \frac{{1700}}{7}\).
Doanh thu được khi công ty sản xuất và tiêu thụ hết \(x\) sản phẩm là \(R\left( x \right) = xp\left( x \right) = 1700x - 7{x^2}\)
Do đó, lợi nhuận thu được là
\(P\left( x \right) = xp\left( x \right) - C\left( x \right)\)\( = 1700x - 7{x^2} - \left( {16\,000 + 500x - 1,6{x^2} + 0,004{x^3}} \right)\)
\(P\left( x \right) = - 0,004{x^3} - 5,4{x^2} + 1200x - 16\,000\), \(0 < x < \frac{{1700}}{7}\).
\(P'\left( x \right) = - 0,012{x^2} - 10,8x + 1200\); \(P'\left( x \right) = 0 \Leftrightarrow - 0,012{x^2} + 10,8x + 1200 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1000\\x = 100\end{array} \right.\).
Đối chiếu điều kiện ta có \(x = 100\).
Lập bảng biến thiên của hàm số, ta thu được kết quả là \(\mathop {\max }\limits_{\left( {0;\frac{{1700}}{7}} \right)} P\left( x \right) = P\left( {100} \right) = 46\,000\) (triệu).
Vậy công ty cần sản xuất 100 sản phẩm thì lợi nhuận thu được là cao nhất.
Đáp án: 100.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1758958917.png)