Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ \[mg/l\]của thuốc trong máu sau \[x\]phút được xác định bởi công thức: \[C(x) = \frac{{30x}}{{{x^2} + 2}}\].
. Calculus. Cengage Learning)
Để đưa ra những lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm khoảng thời gian mà nồng độ của thuốc trong máu đang tăng. Em hãy cho biết hàm nồng độ thuốc trong máu \[C(x)\] đạt giá trị cực đại là bao nhiêu trong khoảng thời gian \[6\] phút sau khi tiêm ?
Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ \[mg/l\]của thuốc trong máu sau \[x\]phút được xác định bởi công thức: \[C(x) = \frac{{30x}}{{{x^2} + 2}}\].

. Calculus. Cengage Learning)
Để đưa ra những lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm khoảng thời gian mà nồng độ của thuốc trong máu đang tăng. Em hãy cho biết hàm nồng độ thuốc trong máu \[C(x)\] đạt giá trị cực đại là bao nhiêu trong khoảng thời gian \[6\] phút sau khi tiêm ?Quảng cáo
Trả lời:
Trả lời: \[10,6\]\[\left( {mg/l} \right)\].
Xét hàm số \[y = C(x) = \frac{{30x}}{{{x^2} + 2}}\] trên khoảng \[x \in \left( {0\,;6} \right)\].
Ta có: \[y' = \frac{{ - 30{x^2} + 60}}{{{{\left( {{x^2} + 2} \right)}^2}}}\].
\[y' = 0 \Leftrightarrow \frac{{ - 30{x^2} + 60}}{{{{\left( {{x^2} + 2} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 \\x = - \sqrt 2 \,\end{array} \right.\]do \[x \in \left( {0\,;6} \right)\]\[ \Rightarrow x = \sqrt 2 \].
Bảng biến thiên:
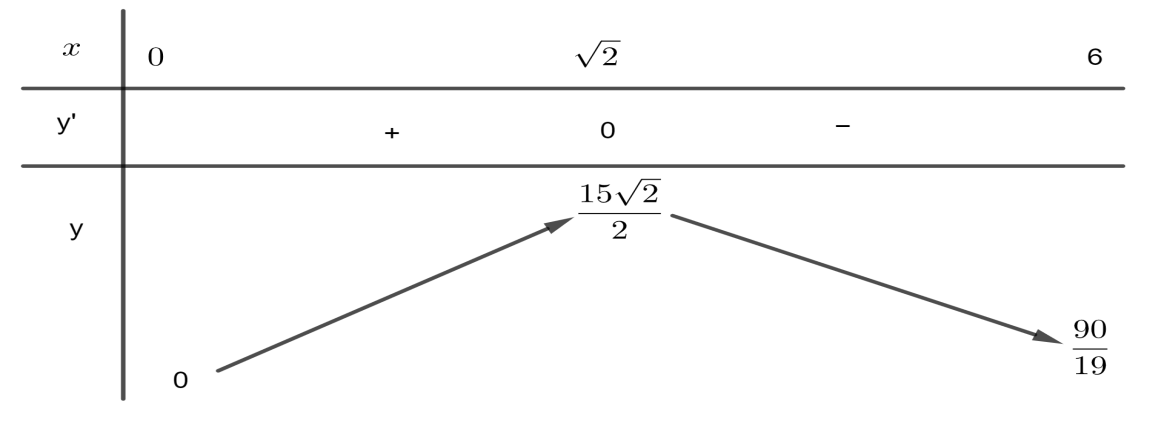
Từ bảng biến thiên suy ra: nồng độ thuốc trong máu \[C\left( x \right)\] đạt giá trị cực đại là \[\frac{{15\sqrt 2 }}{2}\left( {mg/l} \right) \approx 10,6\left( {mg/l} \right)\] trong khoảng thời gian 6 phút sau khi tiêm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
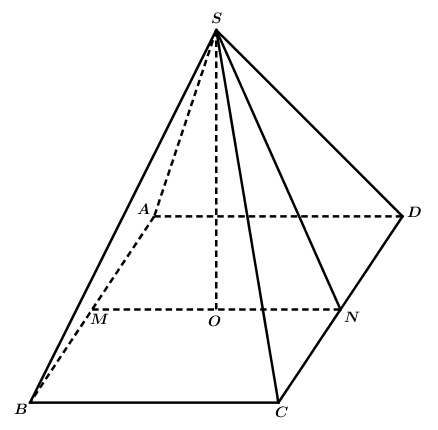
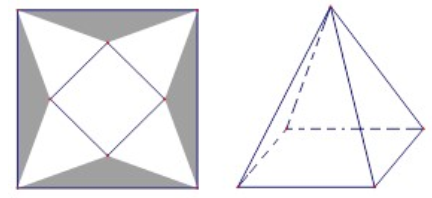
Gọi cạnh đáy hình vuông của tháp là \(x\left( m \right)\).
Độ dài đường chéo tấm bạt bằng \(20\sqrt 2 \,\left( m \right)\).
Gọi hình chóp tứ giác đều là \(S.ABCD\), Gọi\(M,N\) lần lượt là trung điểm \(AB,CD\).
Khi đó \(MN = x\left( m \right)\), \(SN = \frac{{20\sqrt 2 - x}}{2}\left( m \right)\) với \(0 < x < 10\sqrt 2 \).
Gọi \(O\) là tâm của hình vuông, ta có
\(SO = \sqrt {S{N^2} - O{N^2}} = \sqrt {{{\left( {\frac{{20\sqrt 2 - x}}{2}} \right)}^2} - {{\left( {\frac{x}{2}} \right)}^2}} = \frac{1}{2}\sqrt {800 - 40\sqrt 2 x} \).
Thể tích khối chóp \(V = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{6}{x^2}\sqrt {800 - 40\sqrt 2 x} \).
Ta có \(V' = \frac{{20x\left( {80 - 5\sqrt 2 x} \right)}}{{6\sqrt {800 - 40\sqrt 2 x} }}\)
\( \Rightarrow V' = 0 \Leftrightarrow x = 8\sqrt 2 \) với \(0 < x < 10\sqrt 2 \).
Xét bảng biến thiên:
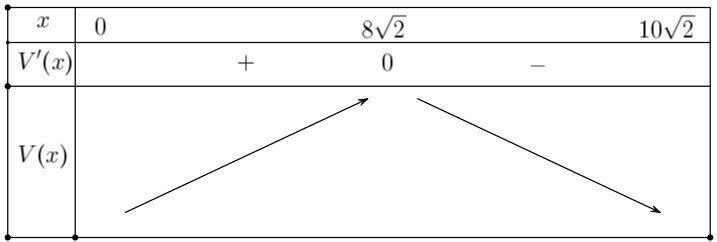
Vậy khi \(x = 8\sqrt 2 \) thì thể tích khối chóp lớn nhất \(V = \frac{{256\sqrt {10} }}{3}\left( {{m^3}} \right)\).
Diện tích phần bị cắt của tấm bạt:
\(S = {S_{hv}} - {S_{ABCD}} - 4.{S_{\Delta SAB}} = {20^2} - {\left( {8\sqrt 2 } \right)^2} - 4.\frac{1}{2}.\frac{{20\sqrt 2 - 8\sqrt 2 }}{2}.8\sqrt 2 = 80\left( {{m^2}} \right)\).
Lời giải
Tập xác định: \[\mathbb{R}\backslash \left\{ { - 1} \right\}\].
Ta có: \(y' = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}}\), \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\).
Bảng xét dấu của \(y'\):
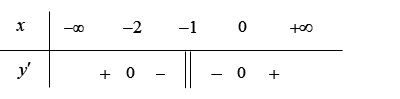
Vậy hàm số nghịch biến trên mỗi khoảng \(\left( { - 2\,;\, - 1} \right)\) và \(\left( { - 1\,;\,0} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Tìm tất cả các khoảng đồng biến của hàm số \[y = f\left( {2 - {x^2}} \right)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759133388.png)
![Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \(\left( { - \infty \,;\,0} \right)\), (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/screenshot-3626-1759133053.png)