Một màn hình chữ nhật cao \(1,4{\rm{m}}\) và đặt ở độ cao \(1,8{\rm{m}}\) so với tầm mắt .

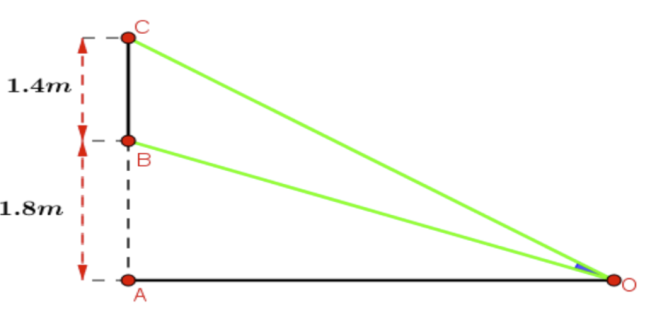
Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn nhất. Tính khoảng cách từ vị trí đó đến màn hình? Biết rằng góc \(\widehat {BOC}\) nhọn.

Đặt độ dài \(OA = x\left( {\rm{m}} \right)\) với \(x > 0\). Ta có: \(OB = \sqrt {{x^2} + 3,24} \); \(OC = \sqrt {{x^2} + 10,24} \)

Sử dụng định lí cosin trong tam giác \(OBC\):

\(\cos \widehat {BOC} = \frac{{O{B^2} + O{C^2} - B{C^2}}}{{2.OB.OC}} = \frac{{{x^2} + 3,24 + {x^2} + 10,24 - 1.96}}{{2\sqrt {{x^2} + 3,24} .\sqrt {{x^2} + 10,24} }}\)

                                                \( = \frac{{{x^2} + 5,76}}{{\sqrt {\left( {{x^2} + 3,24} \right)\left( {{x^2} + 10,24} \right)} }}\).

Vì góc \(\widehat {BOC}\) nhọn nên \(\widehat {BOC}\) lớn nhất khi và chỉ khi \(\cos \widehat {BOC}\) nhỏ nhất. Khi đó bài toán trở thành tìm \(x\) để \(f\left( x \right) = \frac{{{x^2} + 5,76}}{{\sqrt {\left( {{x^2} + 3,24} \right)\left( {{x^2} + 10,24} \right)} }}\) đạt giá trị nhỏ nhất.

Đặt \(t = {x^2} + 3,24\) với \(t > 3,24\). Suy ra \(f\left( t \right) = \frac{{t + \frac{{63}}{{25}}}}{{\sqrt {t\left( {t + 7} \right)} }}\) với \(t \in \left( {3,24; + \infty } \right)\).

Ta có: \(f'\left( t \right) = \frac{1}{{25}}\left( {\frac{{49t - 441}}{{2t\left( {t + 7} \right)\sqrt {t\left( {t + 7} \right)} }}} \right)\).

Cho \(f'\left( x \right) = 0 \Leftrightarrow 49t - 441 = 0 \Leftrightarrow t = 9\).

Bảng biến thiên:

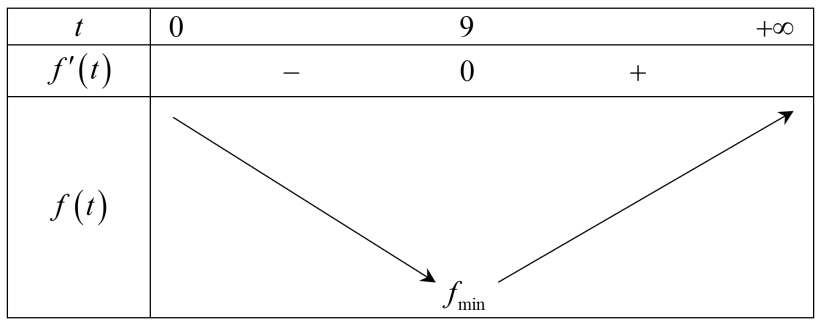
Thế vào biểu thức của phép đặt ta có: \({x^2} + 3,24 = 9 \Leftrightarrow {x^2} = \frac{{144}}{{25}} \Rightarrow x = 2,4{\rm{m}}\).

Vậy để nhìn rõ nhất thì khoảng cách từ vị trí đó đến màn hình là \(OA = 2,4{\rm{m}}\).