PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
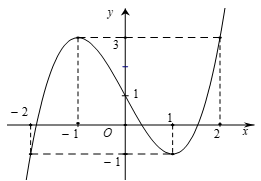
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong như trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Quảng cáo
Trả lời:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 32,6
Để nồng độ chất độc trong máu thấp nhất khi thời gian di chuyển về đến tại thấp nhất.
Vậy nên Quãng đường ông Vinh di chuyển về đến trại phải thấp nhất.
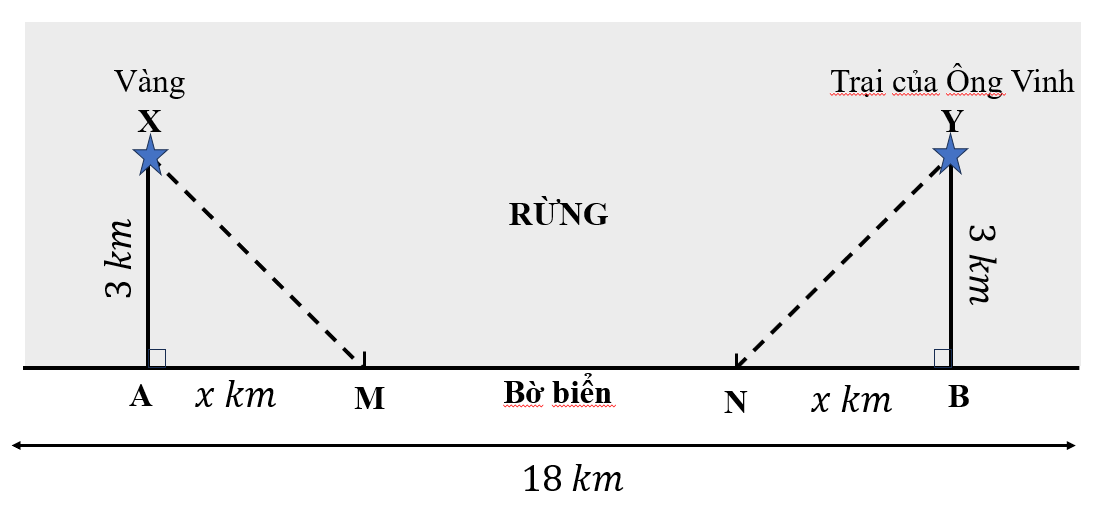
Quãng đường của Ông Vinh
Theo bài ra ta có: ông Vinh sẽ đi qua các quãng đường \[XM + MN + NY.\]
Ta có: \[XM = NY = \sqrt {9 + {x^2}} \]; \[MN = 18 - 2x\]
Thời gian Ông Vinh chạy đến Trại nghỉ là: \[T(x) = 2\left( {\frac{{\sqrt {9 + {x^2}} }}{5} + \frac{{9 - x}}{{13}}} \right)\] với \[x \in \left( {0;9} \right)\]
Xét \[T'(x) = 2\left( {\frac{{\sqrt {9 + {x^2}} }}{5} + \frac{{9 - x}}{{13}}} \right) = 0 \Leftrightarrow x = \frac{5}{4}\] ( thỏa mãn)
Bảng biến thiên:
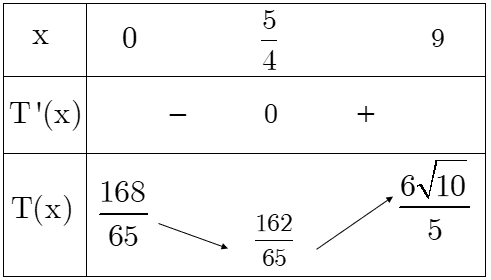
Dựa vào bảng biến thiên, ta thấy giá trị của \(T(x)\) nhỏ nhất khi \(x = \frac{5}{4}\).
\[ \Rightarrow \mathop {Min}\limits_{x \in \left( {0,9} \right)} {\rm{ }}T(x) = T(\frac{5}{4}) = \frac{{162}}{{65}}\]
Vậy, nồng độ chất độc trong máu thấp nhất là \[\mathop {\min }\limits_{(0, + \infty )} y = 50\log \left( {\frac{{162}}{{65}} + 2} \right) \approx 32,6\]
Lời giải
Đáp án: 49,5
Theo bài ra ta có: phương trình của Parabol là \[y = 60 - \frac{3}{{80}}{x^2}\].
Khoảng cách giữa khung Parabol và đường xuyên núi là:
\[D = 60 - \frac{3}{{80}}{x^2} - \left( {\frac{{{x^3}}}{{25600}} - \frac{{3x}}{{16}} + 35} \right)\] với \[x \in \left( { - 23,71;27,99} \right)\]
Xét \[D' = - \frac{3}{{40}}x - \frac{{3{x^2}}}{{25600}} + \frac{3}{{16}} = 0 \Leftrightarrow x = 2,49\]
Bảng biến thiên:
![Hai cột đỡ dọc \[MN\] và \[PQ\] ( song song với trục \[Oy\]) là đoạn nối giữa khung của Parabol và đường \[XY\]. Tính tổng độ d (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759200546.png)
Dựa vào bảng biến thiên, \[MN\] là đoạn có độ dài lớn nhất khi \[x = 2,49\]\[ \Rightarrow MN = {D_{MN}} = 60 - \frac{3}{{80}}.2,{49^2} - \left( {\frac{{2,{{49}^3}}}{{25600}} - \frac{{3.2,49}}{{16}} + 35} \right) \approx 25,23\]
Vì \[N\]và \[Q\] là hai điểm đối xứng qua \[Oy\]\[ \Rightarrow {x_{PQ}} \approx - 2,49\]
\[ \Rightarrow PQ = {D_{PQ}} = 60 - \frac{3}{{80}}.2,{49^2} - \left( {\frac{{ - 2,{{49}^3}}}{{25600}} - \frac{{3. - 2,49}}{{16}} + 35} \right) \approx 24,3\]
Tổng độ dài \[MN + PQ = 49,5\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Hai cột đỡ dọc \[MN\] và \[PQ\] ( song song với trục \[Oy\]) là đoạn nối giữa khung của Parabol và đường \[XY\]. Tính tổng độ d (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759200516.png)
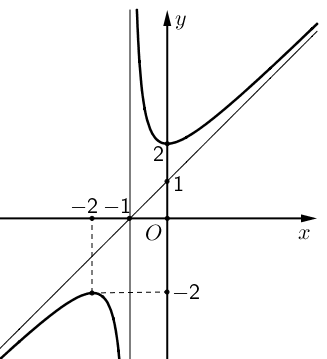
![Cho hàm số hữu tỉ \[y = ax + 2 + \frac{b}{{x + c}}\] có đồ thị như hình bên dưới. Tính\(P = a + b + c.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/12-1759200440.png)