Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh tại thời điểm xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(f\left( t \right) = 4{t^3} - \frac{{{t^4}}}{2}\) (người). Nếu xem \(f'\left( t \right)\) là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\)với \(t \in \left[ {0;6} \right]\). Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?

Hàm số đã cho xác định và liên tục trên \(\left( { - \infty ; - 1} \right) \cup \left( { - 1; + \infty } \right)\)

\(y = \frac{{m{x^2} + \left( {{m^2} + m + 2} \right)x + {m^2} + 3}}{{x + 1}} = mx + {m^2} + 2 + \frac{1}{{x + 1}},x \ne  - 1\)

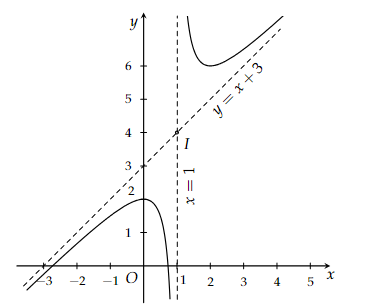
Vì \(\mathop {\lim }\limits_{x \to  - \infty } \frac{1}{{x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{1}{{x + 1}} = 0\) nên \(\left( d \right):y = mx + {m^2} + 2\) \( \Leftrightarrow \left( d \right):mx - y + {m^2} + 2 = 0\) là đường cận xiên hoặc ngang của hàm số.

Ta có: \(d\left( {O;d} \right) = \frac{{\left| {{m^2} + 2} \right|}}{{\sqrt {{m^2} + 1} }} = \sqrt {{m^2} + 1}  + \frac{1}{{\sqrt {{m^2} + 1} }} \ge 2\)

Vậy \(d\left( {O;d} \right)\) nhỏ nhất bằng \(2\) khi \(\sqrt {{m^2} + 1}  = \frac{1}{{\sqrt {{m^2} + 1} }} \Leftrightarrow m = 0\).

Khi đó hàm số có tiệm cận ngang là \(y = 2\).

Ta có\(y' = 3{x^2} - 6x - m\).

Hàm số đồng biến trên khi \(y' \ge 0,\;\forall x \in \left( {0; + \infty } \right) \Leftrightarrow 3{x^2} - 6x - m \ge 0,\;\forall x \in \left( {0; + \infty } \right)\)

\( \Leftrightarrow 3{x^2} - 6x \ge m,\;\forall x \in \left( {0; + \infty } \right)\;\quad \left( 1 \right)\)

Xét hàm số \(f\left( x \right) = 3{x^2} - 6x\;\)trên \(\left( {0; + \infty } \right)\)

Ta có \(f'\left( x \right) = 6x - 6\,,\;f'\left( x \right) = 0 \Leftrightarrow x = 1.\) Do đó \[\mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right) = f\left( 1 \right) =  - 3\]

\(\left( 1 \right) \Leftrightarrow m \le  - 3.\)Kết hợp với giả thiết ta được \(m \in \left( { - 2024; - 3} \right]\). Nên có \[2021\] số nguyên thỏa mãn.