Bác An có một mảnh đất ruộng và muốn dành ra một khu đất hình chữ nhật có diện tích \(242\,{m^2}\) để trồng cây thuốc. Bác dự kiến rào quanh ba cạnh của khu đất hình chữ nhật này bằng lưới thép, cạnh còn lại (chiều dài) sẽ tận dụng bức tường có sẵn. Biết chiều rộng khu đất không vượt quá \(16\,m\). Hỏi chiều rộng của khu đất bằng bao nhiêu để tổng chiều dài lưới thép cần dùng là ngắn nhất (nghĩa là chi phí rào lưới thép thấp nhất)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Gọi chiều rộng khu đất hình chữ nhật cần rào là \(x\,\left( m \right),\,\,0 < x \le 16\).
Diện tích khu đất này là \(242\,{m^2}\) nên chiều dài của khu đất là \(\frac{{242}}{x}\,\,\left( m \right)\)
Tổng chiều dài lưới thép rào quanh khu đất hình chữ nhật là \(2x + \frac{{242}}{x}\,\,\left( m \right)\)
Xét hàm số \(y = 2x + \frac{{242}}{x}\,\,,\,\,x \in \left( {0\,;\,16} \right]\)
Ta có \(y' = 2 - \frac{{242}}{{{x^2}}} = \frac{{2{x^2} - 242}}{{{x^2}}}\) và \(y' = 0 \Rightarrow 2{x^2} - 242 = 0 \Rightarrow x = 11\) (do \(x \in \left( {0\,;\,16} \right]\))
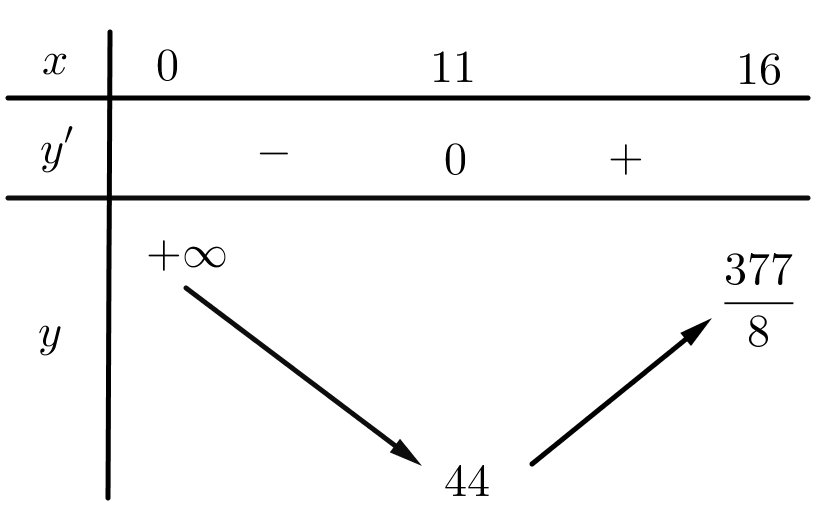
Ta có \(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \left( {2x + \frac{{242}}{x}} \right) = + \infty \,\,;\,\,y\left( {11} \right) = 44;\,\,y\left( {16} \right) = \frac{{377}}{8}\)
Bảng biến thiên
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
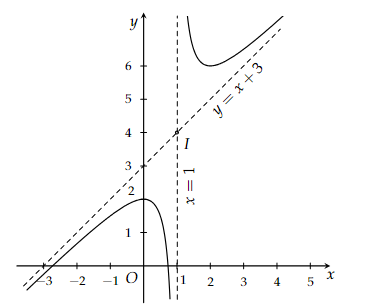
Hàm số đã cho xác định và liên tục trên \(\left( { - \infty ; - 1} \right) \cup \left( { - 1; + \infty } \right)\)
\(y = \frac{{m{x^2} + \left( {{m^2} + m + 2} \right)x + {m^2} + 3}}{{x + 1}} = mx + {m^2} + 2 + \frac{1}{{x + 1}},x \ne - 1\)
Vì \(\mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 1}} = 0\) nên \(\left( d \right):y = mx + {m^2} + 2\) \( \Leftrightarrow \left( d \right):mx - y + {m^2} + 2 = 0\) là đường cận xiên hoặc ngang của hàm số.
Ta có: \(d\left( {O;d} \right) = \frac{{\left| {{m^2} + 2} \right|}}{{\sqrt {{m^2} + 1} }} = \sqrt {{m^2} + 1} + \frac{1}{{\sqrt {{m^2} + 1} }} \ge 2\)
Vậy \(d\left( {O;d} \right)\) nhỏ nhất bằng \(2\) khi \(\sqrt {{m^2} + 1} = \frac{1}{{\sqrt {{m^2} + 1} }} \Leftrightarrow m = 0\).
Khi đó hàm số có tiệm cận ngang là \(y = 2\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có\(y' = 3{x^2} - 6x - m\).
Hàm số đồng biến trên khi \(y' \ge 0,\;\forall x \in \left( {0; + \infty } \right) \Leftrightarrow 3{x^2} - 6x - m \ge 0,\;\forall x \in \left( {0; + \infty } \right)\)
\( \Leftrightarrow 3{x^2} - 6x \ge m,\;\forall x \in \left( {0; + \infty } \right)\;\quad \left( 1 \right)\)
Xét hàm số \(f\left( x \right) = 3{x^2} - 6x\;\)trên \(\left( {0; + \infty } \right)\)
Ta có \(f'\left( x \right) = 6x - 6\,,\;f'\left( x \right) = 0 \Leftrightarrow x = 1.\) Do đó \[\mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right) = f\left( 1 \right) = - 3\]
\(\left( 1 \right) \Leftrightarrow m \le - 3.\)Kết hợp với giả thiết ta được \(m \in \left( { - 2024; - 3} \right]\). Nên có \[2021\] số nguyên thỏa mãn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình sau. Phương trình \[f\left( {f\left( x \right)} \right) = 0\] có bao nhiêu nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759203193.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập