Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Hai đội công nhân cùng làm chung một công việc thì sau \[15\] ngày làm xong. Nếu đội thứ nhất làm riêng trong \[3\] ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó trong \[5\] ngày thì cả hai đội hoàn thành được \[25\% \] công việc. Hỏi mỗi đội làm riêng thì trong bao nhiêu ngày mới xong công việc trên?

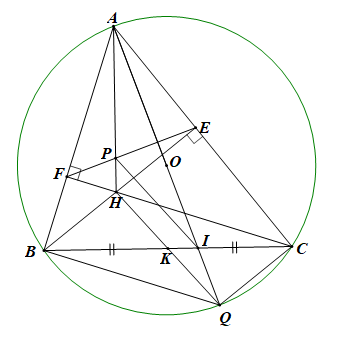
Chứng minh bốn điểm \(B\), \(C\), \(E\), \(F\) cùng thuộc một đường tròn.

Vẽ đúng hình đến ý 1)

Xét tứ giác \(BCEF\) ta có:

\(\widehat {BEC} = 90^\circ \)(\(BE\) là đường cao)

\(\widehat {BFC} = 90^\circ \) (\(CF\) là đường cao)

\( \Rightarrow BCEF\) là tứ giác nội tiếp (đỉnh \(E\), \(F\) cùng nhìn cạnh \(BC\) dưới một góc vuông).

Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \[EF\].

Do tứ giác \(BCEF\) nội tiếp \[ \Rightarrow \widehat {AEF} = \widehat {ABC}\] (vì cùng bù với \(\widehat {FEC}\))

Kẻ đường kính \(AQ\)

\( \Rightarrow \Delta AQC\) vuông tại \(C\)

\( \Rightarrow \widehat {QAC} + \widehat {AQC} = 90^\circ \)

Xét \(\left( O \right)\) có

\[ \Rightarrow \widehat {AEF} + \widehat {EAO} = 90^\circ  \Rightarrow AO \bot EF\]

Chứng minh tam giác \(APE\) đồng dạng với tam giác \(AIB\) và đường thẳng \(KH\) song song với đường thẳng \(IP\).

\(\widehat {EAO} = \widehat {HAB}\) (vì cùng phụ với \(\widehat {ABC}\)) \( \Rightarrow \widehat {EAP} = \widehat {IAB}\)

\(\widehat {AEP} = \widehat {ABI}\)

\[\left( 1 \right)\]

\( \Rightarrow \frac{{AE}}{{AB}} = \frac{{AH}}{{AQ}}\) \(\left( 2 \right)\)

Từ (1) và (2) suy ra \(\frac{{AP}}{{AI}} = \frac{{AH}}{{AQ}} \Rightarrow \frac{{AP}}{{AH}} = \frac{{AI}}{{AQ}} \Rightarrow PI\,{\rm{//}}\,HQ\) \(\left( 3 \right)\)

Xét tứ giác \(BHCQ\) có:

\(BH\,{\rm{//}}\,CQ\) (vì cùng vuông góc với \(AC\))

\(BQ\,{\rm{//}}\,CH\) (vì cùng vuông góc với \(AB\))

\( \Rightarrow BHCQ\) là hình bình hành

\( \Rightarrow BC,HQ\) cắt nhau tại trung điểm của mỗi đường

Mà \(K\) là trung điểm của \(BC\) nên \(K\) là trung điểm của \(HQ\)

\( \Rightarrow H,K,Q\) thẳng hàng (4)

Từ (3) và (4) suy ra \(KH\,{\rm{//}}\,IP\).

Cho biểu thức \[P = {a^4} + {b^4} - ab\], với \[a,b\] là các số thực thỏa mãn \[{a^2} + {b^2} + ab = 3\]. Tìm giá trị lớn nhất, giá trị nhỏ nhất của \[P\].

Số mét khối nước đựng được của bồn chính là thể tích của bồn chứa.

Bồn nước đựng được số mét khối nước là:

\[0,32.1,75 = 0,56\,\,\left( {{m^3}} \right).\]