Quảng cáo
Trả lời:
Giải bởi Vietjack
\(B = \sqrt {9 - 4\sqrt 5 } - \sqrt 5 \)
\( = \sqrt {{{\left( {\sqrt 5 } \right)}^2} - 2.\sqrt 5 .2 + {2^2}} - \sqrt 5 \)
\( = \sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} - \sqrt 5 \)
\( = \left| {\sqrt 5 - 2} \right| - \sqrt 5 \)
\( = \sqrt 5 - 2 - \sqrt 5 \) (do \[\sqrt 5 - 2 > 0\])
\( = - 2\).
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \(x\)(xe) là số xe ban đầu (điều kiện \(x\) nguyên dương).
Lượng gạo mỗi xe phải chở lúc đầu là \(\frac{{160}}{x}\) (tấn).
Số xe sau khi bổ sung \(4\) chiếc là: \(x + 4\) (chiếc xe).
Lượng gạo mỗi xe phải chở sau khi bổ sung là: \(\frac{{160}}{{x + 4}}\) (tấn).
Vì sau khi bổ sung 4 xe thì mỗi xe chở ít hơn dự định 2 tấn nên ta có phương trình:
\(\frac{{160}}{x} - \frac{{160}}{{x + 4}} = 2\)
\( \Rightarrow 160\left( {x + 4} \right) - 160x = 2x\left( {x + 4} \right)\)
\( \Leftrightarrow {x^2} + 4x - 320 = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 16(tm)}\\{x = - 20(ktm)}\end{array}} \right.\)
Vậy ban đầu có \(16\) chiếc xe.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
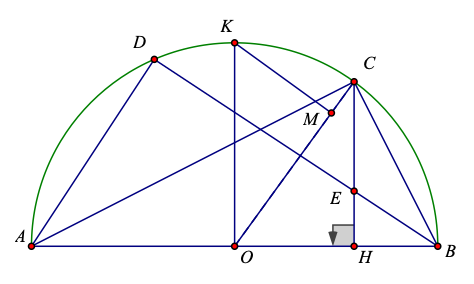
a) Ta có \(\widehat {ADE} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) và \(\widehat {AHE} = 90^\circ \) (\(H\) là hình chiếu vuông góc của \(C\) trên \(AB\))
\( \Rightarrow \widehat {ADE} + \widehat {AHE} = 180^\circ \).
Vậy tứ giác \(ADEH\) nội tiếp.
b) Ta có: \(\widehat {ACO} = \widehat {CAO}\) (tam giác \(AOC\) cân tại \(O\)).
Mà \(\widehat {CAO} = \widehat {HCB}\) (cùng phụ \(\widehat {ABC}\))
Vậy \(\widehat {ACO} = \widehat {HCB}\).
Xét \(\Delta ACB\) và \(\Delta CHB\) có:
\(\left\{ \begin{array}{l}\widehat {CAO} = \widehat {HCB}\left( {{\rm{cmt}}} \right)\\\widehat {ACB} = \widehat {CHB\,\,}\left( { = 90^\circ } \right)\end{array} \right.\)
\( \Rightarrow \frac{{AC}}{{CH}} = \frac{{CB}}{{HB}}\) (các cặp cạnh tương ứng tỉ lệ).
\( \Rightarrow AC.HB = CB.CH\)
\( \Rightarrow AC.\left( {AB - AH} \right) = CB.CH\)
\( \Rightarrow AC.AB = AC.AH + CB.CH\).
c) Gọi \(K\) là điểm chính giữa cung \(AB\), ta có \(OK \bot OB\) suy ra \(OK\)//\(CH\).
\( \Rightarrow \widehat {KOM} = \widehat {OCH}\) (2 góc so le trong).
Xét \(\Delta OMK\)và \(\Delta CHO\) có:
\(\left\{ \begin{array}{l}OM = CH\left( {{\rm{gt}}} \right)\\\widehat {KOM} = \widehat {OCH}\left( {{\rm{cmt}}} \right)\\OK = OC\,\,\,\,\,\left( {{\rm{b\'a n}}\,\,{\rm{k\'i nh}}} \right)\end{array} \right.\)
\[ \Rightarrow \Delta OMK = \Delta CHO{\rm{ }}\left( {{\rm{c}}{\rm{.g}}{\rm{.c}}} \right)\]
\( \Rightarrow \widehat {KMO} = \widehat {CHO} = 90^\circ \).
Do đó, góc \[KMO\] luôn nhìn cạnh \[OK\] dưới một góc vuông nên \[M\] thuộc đường tròn đường kính \(OK\).
Vì nửa đường tròn tâm \(O\) đường kính \(AB\) cố định nên điểm chính giữa cung \(AB\) là \[K\] cố định hay \[OK\] luôn cố định.
Vậy khi \(C\) di chuyển trên nửa đường tròn \[\left( O \right)\] thì \(M\) chạy trên đường tròn đường kính (OK\)cố định.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập