Cho biểu thức \(B = \sqrt {9x + 9}  + \sqrt {4x + 4}  + \sqrt {x + 1} \) với \(x \ge  - 1.\) Tìm \(x\)sao cho \(B\) có giá trị là \(18\).

a) • Vẽ đồ thị hàm số \(y = 2{x^2}\):

Hàm số \(y = 2{x^2}\) có hệ số \(a = 2 > 0\) nên hàm số đồng biến khi \(x > 0\), nghịch biến khi \(x < 0\) và đồ thị hàm số là parabol có bề lõm quay lên trên, nhận trục \(Oy\) làm trục đối xứng.

Bảng giá trị:

Vậy đồ thị hàm số \(y = 2{x^2}\) là parabol đi qua các điểm \(\left( { - 2;8} \right),\left( { - 1;2} \right),\left( {0;0} \right),\left( {1;2} \right),\left( {2;8} \right)\).

• Vẽ đồ thị hàm số \(y =  - 2x + 4\):

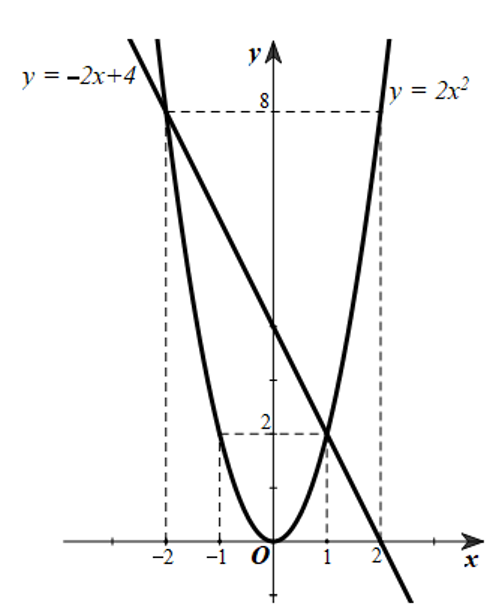
Cho \(x = 0\) thì \(y = 4\), ta được điểm \(\left( {0;4} \right)\).

Cho \(y = 0\) thì \(x = 2\), ta được điểm \(\left( {2;0} \right)\).

Đồ thị hàm số \(y =  - 2x + 4\) là đường thẳng đi qua 2 điểm trên.

Ta vẽ các đồ thị hàm số \(y = 2{x^2}\) và \(y =  - 2x + 4\) trên cùng một mặt phẳng tọa độ như sau:

b) Xét phương trình hoành độ giao điểm của đường thẳng \(y =  - 2x + 4\)và parabol \(y = 2{x^2}\):

\( \Leftrightarrow {x^2} + x - 2 = 0\)

\( \Leftrightarrow {x^2} - x + 2x - 2 = 0\)

\( \Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 2\end{array} \right.\)

Với \(x = 1 \Rightarrow y = 2\)

Với \(x =  - 2 \Rightarrow y = 8\)

Vậy giao điểm của hai đồ thị hàm số đã cho là \(A\left( {1;2} \right);B\left( { - 2;8} \right)\).

* Tính khoảng cách từ \(M\left( { - 2;0} \right)\) đến đường thẳng \[AB\].

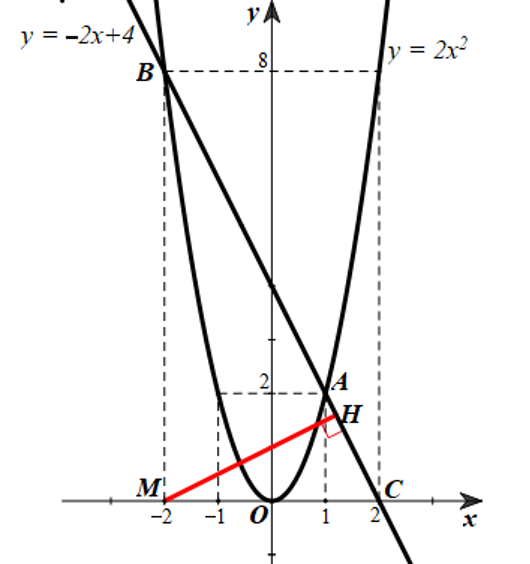
Kẻ \(MH \bot AB\left( {M \in AB} \right).\)

Do đó khoảng cách từ \(M\left( { - 2;0} \right)\) xuống đường thẳng \[AB\] chính là độ dài đoạn thẳng \(MH.\)

Gọi \(C\) là giao điểm của \(AB\) và \(Ox\) \( \Rightarrow C\left( {2;0} \right)\).

Dễ thấy \(\Delta MAC\) vuông tại \(M\), \(MA = 8,MC = 4\)

Áp dụng hệ thức lượng cho tam giác vuông \(\Delta MAC\), ta có:

\(\frac{1}{{M{H^2}}} = \frac{1}{{M{A^2}}} + \frac{1}{{M{C^2}}} = \frac{1}{{{8^2}}} + \frac{1}{{{4^2}}} = \frac{5}{{64}}\)

\( \Leftrightarrow MH = \frac{{8\sqrt 5 }}{5}\) (đơn vị dài)

Vậy khoảng cách cần tìm là \(MH = \frac{{8\sqrt 5 }}{5}\).

Gọi chiều rộng của mảnh đất là \(x\) (mét) \(\left( {x > 3} \right)\).

Chiều dài của mảnh đất là \(y\) (mét) \(\left( {y > x > 3} \right)\).

Diện tích mảnh đất là \(80{m^2}\) nên ta có phương trình \(xy = 80\,\,\,\,\left( 1 \right)\)

Nếu giảm chiều rộng đi \(3m\) thì chiều rộng mới là \(x - 3\) (mét).

Nếu tăng chiều dài lên \(10m\) thì chiều dài mới là \(y + 10\) (mét).

Diện tích mảnh đất mới là \(80 + 20 = 100\,\left( {{m^2}} \right)\), khi đó ta có phương trình:

\(\left( {x - 3} \right)\left( {y + 10} \right) = 100\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{ \begin{array}{l}xy = 80\\\left( {x - 3} \right)\left( {y + 10} \right) = 100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}xy = 80\\xy - 3y + 10x - 30 - 100 = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}xy = 80\\80 + 10x - 3y - 130 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}10xy = 800\\10x = 3y + 50\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {3y + 50} \right)y = 800\\10x = 3y + 50\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}3{y^2} + 50y - 800 = 0\\10x = 3y + 50\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}y = 10(tm)\\y =  - \frac{{80}}{3}(ktm)\end{array} \right.\\10x = 3y + 50\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 8\\y = 10\end{array} \right.(tm)\)

Vậy chiều dài mảnh đất là 10\(m\) và chiều rộng mảnh đất là \(8m\).