Cho vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích I khi A thay đổi.
Câu hỏi trong đề: Bài tập ôn tập chương 3 hình học 9 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
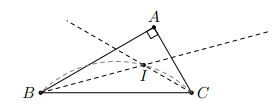
Phần thuận: Ta có:
Vì B, C cố định, A thay đổi, I luôn nhìn cạnh BC dưới một góc nên I di chuyển trên cung chứa góc dựng trên BC.
Phần đảo: Lấy điểm I là giao của cung chứa góc dựng trên BC và tia phân giác trong góc , ta chứng minh I cũng thuộc tia phân giác trong của góc .
Xét tam giác IBC, ta có:
Nên BI là phân giác trong của . Hay I là tâm đường tròn nội tiếp (I là giao điểm của ba đường phân giác trong)
Giới hạn:
- Khi thì ba điểm A, B, C thẳng hàng (trái giả thiết)
- Khi thì ba điểm A, B, C thẳng hàng (trái giả thiết)
Vậy quỹ tích điểm I là cung chứa góc dựng trên cạnh BC đối xứng nhau qua BC, bỏ đi điểm B và C.
Kết luận: Quỹ tích điểm I là cung chứa góc dựng trên cạnh BC đối xứng nhau qua BC, bỏ đi điểm B và C.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
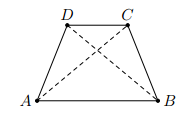
Xét hai tam giác và , ta có:
CD chung
, vì ABCD là hình thang cân.
AD = BC, vì ABCD là hình thang cân.
Do đó:
=>
Vậy các điểm A, B nằm cùng phía đối với CD và thỏa mãn nên bốn điểm A, B, C, D cùng thuộc một đường tròn.
Lời giải
- Phần thuận:
Xét hai tam giác vuông có
BC = CD (do ABCD là hình vuông)
CE = CF (gt) nên
Do đó,
Mà (đối đỉnh) nên
Vậy điểm M nằm trên đường tròn đường kính BD.
- Giới hạn:
+ Nếu
+ Nếu
Vậy điểm M chỉ nằm trên cung nhỏ của đường tròn đường kính BD.
- Phần đảo:
Lấy điểm M trên cung nhỏ của đường tròn đường kính BD. Nối MB, MD lần lượt cắt CD, BC tại F, E
Ta có (góc nội tiếp chắn nửa đường tròn) nên do đó CF = CE.
- Kết luận: quỹ tích điểm M nằm trên cung nhỏ của đường tròn đường kính BD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập