Dạng 5: Chứng minh nhiều điểm thẳng hàng có đáp án
31 người thi tuần này 4.6 7.7 K lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 6 năm 2026-2027 THCS&THPT Lương Thế Vinh (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 6 năm 2024-2025 THCS Nguyễn Công Trứ (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 6 năm 2024-2025 THCS Vạn Phúc (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 6 năm 2024-2025 THCS Phúc Lợi (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 6 năm 2024-2025 THCS Thanh Am (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 6 năm 2024-2025 THCS Thạch Bàn (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 6 năm 2025-2026 THCS Lê Ngọc Hân (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 6 năm 2025-2026 THCS Bát Tràng (Hà Nội) có đáp án
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Theo đề bài, điểm C nằm giữa hai điểm A và D nên ba điểm A, C, D cùng nằm trên một đường thẳng.
Điểm D nằm giữa hai điểm C và B nên ba điểm C, B, D cùng nằm trên một đường thẳng.
Hai đường thẳng này có hai điểm chung là C, D nên chúng phải trùng nhau, suy ra 4 điểm A, B, C, D thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ba điểm A, B, C thẳng hàng nên chúng cùng nằm trên cùng một đường thẳng.
Ba điểm B, C, D thẳng hàng nên chúng cùng nằm trên cùng một đường thẳng.
Hai đường thẳng này có hai điểm chung là B, C nên chúng phải trùng nhau, suy ra bốn điểm A, B, C, D thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
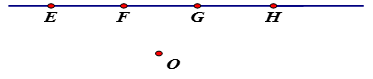
a) Ba điểm E, F, G thẳng hàng nên chúng cùng nằm trên một đường thẳng. Ba điểm F, G, H thẳng hàng nên chúng cùng nằm trên một đường thẳng mà hai đường thẳng này có hai điểm chung là F và G nên hai đường thẳng này phải trung nhau nên bốn điểm E, F, G, H thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
b) Ta có E, F, G, H thẳng hàng theo chứng minh trên nên bốn điểm E, F, G, H cùng nằm trên một đường thẳng. Mặt khác theo bài ra ta có E, F, O không thẳng hàng nên điểm O không nằm trên đường thẳng chứa bốn điểm E, F, G, H. Suy ra ba điểm E, H, O không thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
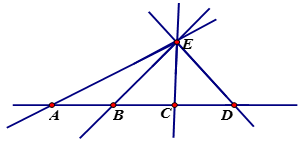
a) Ta có ba điểm A, B, C thẳng hàng nên ba điểm này cùng nằm trên cùng một đường thẳng. Ba điểm B, C, D thẳng hàng nên ba điểm này cũng nằm trên một đường thẳng. Suy ra hai đường thẳng này có hai điểm chung là B và C nên hai đường thẳng này trùng nhau. Vậy 3 điểm A, B, D thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
b) Các đường thẳng trong hình vẽ là: AE, BE, CE, DE và đường thẳng đi qua 4 điểm A, B, C, D gọi chung là đường thẳng AD.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập