Đề thi cuối học kỳ 2 Toán 6 Cánh diều cấu trúc mới có đáp án - Đề 9

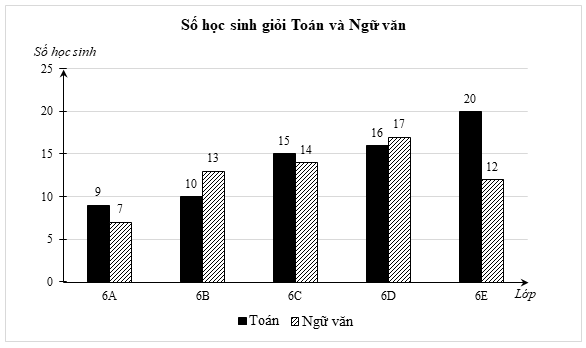
1) a) Số học sinh giỏi Toán của lớp 6E là nhiều nhất (20 bạn).

Số học sinh giỏi Ngữ văn của lớp 6A là ít nhất (7 bạn).

b) Số học sinh giỏi Toán của lớp 6C chiếm số phần trăm trong tổng số học sinh giỏi môn Toán của cả 5 lớp là: \(\frac{{15}}{{9 + 10 + 15 + 16 + 20}} \cdot 100\%  \approx 21,43\% .\)

c) Bạn An nói lớp 6D có sĩ số là 34 học sinh có thể chưa đúng vì trong lớp có thể có học sinh không giỏi môn Toán, hoặc học sinh không giỏi môn Ngữ văn, hoặc học sinh giỏi cả hai môn.

2) Số chấm xuất hiện là số không vượt quá 4 là: 1 chấm, 2 chấm, 3 chấm, 4 chấm.

Số lần xuất hiện mặt có số chấm không vượt quá 4 là: \[15 + 20 + 18 + 22 = 75.\]

Xác suất thực nghiệm của sự kiện số chấm xuất hiện là số không vượt quá 4 là: \(\frac{{75}}{{100}} = \frac{3}{4}.\)

a) \(\frac{9}{{12}} - x =  - \frac{3}{5}\)

\(x = \frac{9}{{12}} - \left( { - \frac{3}{5}} \right)\)

\(x = \frac{3}{4} + \frac{3}{5}\)

\(x = \frac{{27}}{{20}}\)

Chiều rộng của khu vườn là: \(4,5:15\%  = 30{\rm{\;(m)}}{\rm{.}}\)

Diện tích của khu vườn là: \(50 \cdot 30 = 1500{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích đào ao là: \(360:\frac{6}{7} = 420{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích trồng rau là: \(65\%  \cdot \left( {1500 - 420} \right) = 702{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích trồng hoa là: \(1500 - 420 - 702 = 378{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

1)

a) Điểm \(C\) nằm giữa hai điểm \(A\) và \(B\) nên ta có: \(AC + CB = AB\)

Suy ra \(CB = AB - AC = 10 - 5 = 5{\rm{\;cm}}{\rm{.}}\)

b) Ta có điểm \(C\) nằm giữa hai điểm \(A,\) \(B\) và \(AB = BC = \frac{{AB}}{2} = 5\,\,{\rm{cm}}\)

Do đó điểm \[C\] là trung điểm đoạn thẳng \(AB.\)

c) ⦁ Vì điểm \(I\) là trung điểm của \(AC\) nên \(IC = \frac{{AC}}{2} = \frac{5}{2} = 2,5{\rm{\;(cm)}}{\rm{.}}\)

Vì điểm \(F\) là trung điểm của \(CB\) nên \(CF = \frac{{CB}}{2} = \frac{5}{2} = 2,5{\rm{\;(cm)}}{\rm{.}}\)

Ta có điểm \(C\) nằm giữa \(I\) và \(F\) nên \[IF = IC + CF = 2,5{\rm{\;}} + 2,5{\rm{\;}} = 5{\rm{\;(cm)}}{\rm{.}}\]

⦁ Ta có điểm \(C\) nằm giữa \(I\) và \(F\) nên \(IF = IC + CF = \frac{{AC}}{2} + \frac{{CB}}{2} = \frac{{AB}}{2}.\)

Vì độ dài đoạn \(AB\) là không đổi nên độ dài đoạn thẳng \(IF\) không phụ thuộc vào vị trí điểm \(C\) trên đoạn thẳng \(AB.\)

2) a) Ta có \(15^\circ  < 20^\circ  < 25^\circ  < 30^\circ \) nên \[\widehat {yOz} < \widehat {xOy} < \widehat {tOu} < \widehat {zOt}.\]

Do đó ta sắp xếp được các góc đã cho theo thứ tự số đo tăng dần như sau: \[\widehat {yOz},\,\,\widehat {xOy},\,\,\widehat {tOu},\,\,\widehat {zOt}.\]

Ta thấy các góc trên đều có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) nên các góc này đều là góc nhọn.

b) Ta có: \(\widehat {xOu} = \widehat {xOy} + \widehat {yOz} + \widehat {zOt} + \widehat {tOu} = 20^\circ  + 15^\circ  + 30^\circ  + 25^\circ  = 90^\circ \)

Do đó góc \(xOu\) là góc vuông.