Đề thi cuối học kỳ 2 Toán 6 Cánh diều cấu trúc mới có đáp án - Đề 10
17 người thi tuần này 4.6 2 K lượt thi 6 câu hỏi 45 phút
🔥 Đề thi HOT:
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
10 Bài tập Các bài toán thực tế về số nguyên âm (có lời giải)
13 Bài tập Một số bài toán thực tế về hình vuông, hình chữ nhật (có lời giải)
Đề kiểm tra giữa kì 1 Toán 6 Cánh diều có đáp án (Đề 1)
13 Bài tập Tính chu vi và diện tích của hình bình hành, hình thang cân (có lời giải)
10 Bài tập Ứng dụng bội chung và bội chung nhỏ nhất để giải các bài toán thực tế (có lời giải)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
1) Một cửa hàng bán điện thoại lấy ý kiến đánh giá của khách hàng về thái độ phục vụ của nhân viên. Biểu đồ tranh dưới đây là kết quả đánh giá của khách hàng về thái độ phục vụ của nhân viên bán hàng X trong một tuần (mỗi biểu tượng thể hiện kết quả của một lần đánh giá, rất hài lòng: , hài lòng:
, hài lòng: , không hài lòng:
, không hài lòng: ).
).
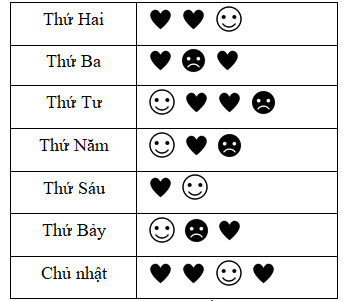
a) Có bao nhiêu lượt khách hàng đã đánh giá về thái độ phục vụ của nhân viên bán hàng X trong một tuần?
b) Có bao nhiêu lượt khách hàng không hài lòng về thái độ phục vụ của nhân viên bán hàng X trong một tuần?
c) Số lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên bán hàng X trong ngày Chủ nhật chiếm bao nhiêu phần trăm so với số lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên bán hàng X trong cả tuần đó?
2) Tung hai đồng xu cân đối 50 lần bạn Mai được kết quả dưới đây, trong đó bạn quên không điền thống kê số lần cả hai đồng xu cùng xuất hiện mặt ngửa:
Sự kiện
Hai đồng ngửa
Một đồng ngửa, một đồng sấp
Hai đồng sấp
Số lần
?
26
14
Tính số lần cả hai đồng xu cùng xuất hiện mặt ngửa từ đó tính xác suất thực nghiệm của sự kiện xuất hiện hai đồng xu là giống nhau.
1) Một cửa hàng bán điện thoại lấy ý kiến đánh giá của khách hàng về thái độ phục vụ của nhân viên. Biểu đồ tranh dưới đây là kết quả đánh giá của khách hàng về thái độ phục vụ của nhân viên bán hàng X trong một tuần (mỗi biểu tượng thể hiện kết quả của một lần đánh giá, rất hài lòng: , hài lòng:
, hài lòng: , không hài lòng:
, không hài lòng: ).
).

a) Có bao nhiêu lượt khách hàng đã đánh giá về thái độ phục vụ của nhân viên bán hàng X trong một tuần?
b) Có bao nhiêu lượt khách hàng không hài lòng về thái độ phục vụ của nhân viên bán hàng X trong một tuần?
c) Số lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên bán hàng X trong ngày Chủ nhật chiếm bao nhiêu phần trăm so với số lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên bán hàng X trong cả tuần đó?
2) Tung hai đồng xu cân đối 50 lần bạn Mai được kết quả dưới đây, trong đó bạn quên không điền thống kê số lần cả hai đồng xu cùng xuất hiện mặt ngửa:
|
Sự kiện |
Hai đồng ngửa |
Một đồng ngửa, một đồng sấp |
Hai đồng sấp |
|
Số lần |
? |
26 |
14 |
Tính số lần cả hai đồng xu cùng xuất hiện mặt ngửa từ đó tính xác suất thực nghiệm của sự kiện xuất hiện hai đồng xu là giống nhau.
Lời giải
1) a) Số lượt khách hàng đã đánh giá về thái độ phục vụ của nhân viên bán hàng X trong một tuần đó là: \(3 + 3 + 4 + 3 + 2 + 3 + 4 = 22\) (lượt).
b) Số lượt khách không hài lòng về thái độ phục vụ của nhân viên bán hàng X trong ngày một tuần đó là: \(1 + 1 + 1 + 1 = 4\) (lượt).
c) Số lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên bán hàng X trong ngày Chủ nhật là: 3 (lượt).
Số lượt khách rất hài lòng về thái độ phục vụ của nhân viên bán hàng X trong ngày một tuần đó là: \(2 + 2 + 2 + 1 + 1 + 1 + 3 = 12\) (lượt).
Tỉ số phần trăm số lượt khách hàng rất hài lòng trong ngày Chủ nhật so với cả tuần là: \(\frac{3}{{12}} \cdot 100\% = 25\% .\)
2) Số lần cả hai đồng xu cùng xuất hiện mặt ngửa là: \(50 - 26 - 14 = 10\) (lần).
Hai đồng xu xuất hiện mặt giống nhau tức là cùng sấp hoặc cùng ngửa.
Vậy xác suất thực nghiệm của sự kiện xuất hiện hai đồng xu giống nhau là: \(\frac{{10 + 14}}{{50}} = \frac{{24}}{{50}} = \frac{{12}}{{25}}.\)
Lời giải
|
a) \(\frac{2}{3} - \left( {\frac{{ - 5}}{7} + \frac{2}{3}} \right)\)\( = \frac{2}{3} + \frac{5}{7} - \frac{2}{3}\) \( = \left( {\frac{2}{3} - \frac{2}{3}} \right) + \frac{5}{7}\)\( = 0 + \frac{5}{7}\)\( = \frac{5}{7}.\) |
b) \[60,7 + 25,5--38,7\] \[ = \left( {60,7--38,7} \right) + 25,5\] \[ = 22 + 25,5\] \( = 47,5.\) |
|
c) \(\frac{2}{3}:\left( {\frac{2}{5} + \frac{1}{2}} \right) + \frac{2}{3}:\left( {\frac{1}{4} - \frac{4}{7}} \right)\) \( = \frac{2}{3}:\frac{9}{{10}} + \frac{2}{3}:\frac{{ - 9}}{{28}}\) \( = \frac{2}{3} \cdot \frac{{10}}{9} + \frac{2}{3} \cdot \frac{{ - 28}}{9}\) \[ = \frac{2}{3} \cdot \left( {\frac{{10}}{9} + \frac{{ - 28}}{9}} \right)\] \( = \frac{2}{3} \cdot \left( { - 2} \right) = \frac{{ - 4}}{3}\). |
d) \[{\left( { - 2} \right)^3} \cdot \frac{{ - 1}}{{24}} + \left( {80\% - 1,2} \right):\frac{2}{{15}}\] \( = \left( { - 8} \right) \cdot \frac{{ - 1}}{{24}} + \left( {\frac{4}{5} - \frac{6}{5}} \right) \cdot \frac{{15}}{2}\) \( = \frac{1}{3} + \frac{{ - 2}}{5} \cdot \frac{{15}}{2}\) \( = \frac{1}{3} + \left( { - 3} \right)\) \( = \frac{1}{3} + \frac{{ - 9}}{3} = \frac{{ - 8}}{3}.\) |
Lời giải
a) \(\frac{1}{6} - x = \frac{{ - 1}}{{42}}\)
\(x = \frac{1}{6} - \frac{{ - 1}}{{42}}\)
\(x = \frac{7}{{42}} + \frac{1}{{42}}\)
\(x = \frac{8}{{42}}\)
\(x = \frac{4}{{21}}\)
Vậy \(x = \frac{4}{{21}}.\)b) \( - 0,6 + x = 0,5\)
\(x = 0,5 - \left( { - 0,6} \right)\)
\(x = 0,5 + 0,6\)
\(x = 1,1.\)
Vậy \(x = 1,1.\)c) \(\frac{1}{2}\left( {x - \frac{2}{3}} \right) - \frac{1}{3}\left( {2x - 3} \right) = x\)
\(\frac{1}{2}x - \frac{1}{3} - \frac{2}{3}x + 1 - x = 0\)
\(\left( {\frac{1}{2}x - \frac{2}{3}x - x} \right) + \left( { - \frac{1}{3} + 1} \right) = 0\)
\(\left( {\frac{1}{2} - \frac{2}{3} - 1} \right)x + \frac{2}{3} = 0\)
\(\frac{{ - 7}}{6}x + \frac{2}{3} = 0\)
\(\frac{{ - 7}}{6}x = - \frac{2}{3}\)
\(x = - \frac{2}{3}:\frac{{ - 7}}{6}\)
\(x = - \frac{2}{3} \cdot \frac{6}{{ - 7}}\)
\(x = \frac{4}{7}\)
Vậy \(x = \frac{4}{7}.\)Lời giải
Số bao xi măng còn lại sau khi đội thứ nhất chở là: \(100\% - 40\% = 60\% \) (tổng số bao).
Số bao xi măng đội thứ hai chở được chiếm:
\(45\% \cdot 60\% = 27\% \) (tổng số bao).
Theo quy định, số bao xi măng đội thứ ba phải chở chiếm:
\(60\% - 27\% = 33\% \) (tổng số bao).
Mà theo quy định, đội thứ ba phải chở là: \(140 - 8 = 132\) (bao).
Tổng số bao cả ba đội phải chở theo quy định là: \(132:33\% = 400\) (bao).
Vậy cả ba đội đã chở được số bao xi măng là: \(400 + 8 = 408\) (bao).
Lời giải
1)
![1) Điểm \(A\) nằm trên tia \(Ox\) sao cho \(OA = 4{\rm{\;cm}}.\) Trên tia đối của tia \(Ox\) lấy điểm \(B\) và \(M\) sao cho \(OB = 8{\rm{\;cm}}\) và \(OM = OA.\) a) Điểm \(O\) có phải là trung điểm của đoạn thẳng \(AM\) không? Tại sao? b) Tính độ dài đoạn thẳng \(BM\) và \(AB.\) c) Gọi \(C\) là trung điểm của đoạn thẳng \(AB.\) Chứng minh \(C\) là trung điểm của đoạn thẳng \(OM.\) 2) a) Góc nhọn, góc vuông có số đo như thế nào? b) Trong các góc sau: \(\widehat {{A_1}} = 90^\circ ,\,\,\widehat {{A_2}} = 10^\circ ,\,\,\widehat {{A_3}} = 40^\circ ,\,\,\widehat {{A_4}} = 45^\circ ,\,\,\widehat {{A_5}} = 120^\circ \) có những góc nào là góc nhọn? Giả sử \[\widehat {{A_6}}\] có số đo bằng tổng số đo các góc nhọn, thì góc \({A_6}\) là loại góc gì? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid12-1751268540.png)
a) Vì điểm \(A\) thuộc tia \[Ox\] và tia \(M\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A,\,\,M.\)
Lại có \(OA = OM\) nên điểm \(O\) là trung điểm của đoạn thẳng \(AM.\)
b) ⦁ Ta có \(OM = OA = 4{\rm{\;cm}}\) và \(OB = 8{\rm{\;cm}}\) nên \(OM < OB\)
Mà hai điểm \(B\) và \(M\) nằm trên tia đối của tia \(Ox\) nên điểm \(M\) nằm giữa hai điểm \(O\) và \(B\)
Do đó \(OB = BM + OM\)
Suy ra \(BM = OB - OM = 8 - 4 = 4{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(A\) thuộc tia \[Ox\] và tia \(B\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A\) và \(B\)
Do đó \(AB = BO + OA = 8 + 4 = 12{\rm{\;(cm)}}{\rm{.}}\)
c) Vì điểm \(C\) là trung điểm của đoạn thẳng \(AB\) nên \(BC = AC = \frac{{AB}}{2} = \frac{{12}}{2} = 6{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(A\) thuộc tia \[Ox\] và tia \(C\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A\) và \(C\)
Do đó \(AC = CO + OA\)
Suy ra \(CO = AC - OA = 6 - 4 = 2{\rm{\;(cm)}}{\rm{.}}\)
⦁ Ta có điểm \(M\) nằm giữa \(C\) và \(B\) nên \(BC = BM + CM\)
Suy ra \(CM = BC - BM = 6 - 4 = 2{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(C\) nằm giữa hai điểm \(M,\,\,O\) và \(MC = CO = 2{\rm{\;cm}}\) nên điểm \(C\) là trung điểm của đoạn thẳng \(OM.\)
2) a) Góc nhọn có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ .\)
Góc vuông có số đo bằng \(90^\circ .\)
b) Ta có: \[0^\circ < 10^\circ < 40^\circ < 45^\circ < 90^\circ < 120^\circ \] hay \[0^\circ < \widehat {{A_2}} < \widehat {{A_3}} < \widehat {{A_4}} < \widehat {{A_1}} = 90^\circ < \widehat {{A_5}}\]
Do đó, trong những góc đã cho, có 3 góc nhọn là: \[\widehat {{A_2}},\,\,\widehat {{A_3}},\,\,\widehat {{A_4}}.\]
Ta có: \[\widehat {{A_6}} = \widehat {{A_2}} + \widehat {{A_3}} + \widehat {{A_4}} = 10^\circ + 40^\circ + 45^\circ = 95^\circ \] và \(90^\circ < 95^\circ < 180^\circ \) nên góc \({A_6}\) là góc tù.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.