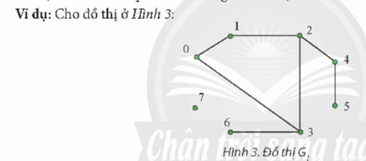
Chuyên đề Tin 12 CTST Bài 3.5. Thực hành kĩ thuật duyệt đồ thị có lời giải

Hai thuật toán duyệt đồ thị theo chiều rộng (BFS) và chiều sâu (DFS) là hai thuật toán cơ bản nhất của đồ thị. Các thuật toán này giúp chúng ta “đến thăm” tất cả các cạnh và các đỉnh của đồ thị trong thời gian tối thiểu. Một số bài toán như: Kiểm tra một đồ thị là phân đôi (bi-partite), Tìm đường ngắn nhất trong đồ thị không có trọng số (Single source Shortest path in an unweighted graph), Tìm vòng trong đồ thị vô hướng, Tìm vòng (cycle) trong đồ thị có hướng,   Case study: Dò mìn (Minesweeper).

Sử dụng thuật toán duyệt đồ thị theo chiều rộng, bắt đầu từ đỉnh u. Em xây dựng mảng một chiều before với giá trị mặc định của các phần tử là −1 để lưu lại các đỉnh trong quá trình duyệt với quy ước: before[i] = j nghĩa là duyệt đỉnh j trước rồi duyệt đỉnh i sau.

Chương trình tìm đường đi sử dụng thuật toán duyệt đồ thị theo chiều rộng:

def initQueue(): return []

def isEmptyQueue(queue): return len(queue) == 0 def enqueue(queue, val): queue.append(val)

def dequeue(queue): return queue.pop(0)

#Hàm xuất đường đi

def printPath(path, u, v): if path == None:

print("Không có đường đi từ đỉnh", ", "đến đỉnh", v)

else:

print("Đường đi từ đỉnh", U, "đến đỉnh", V, "là:") for v in path:

print(v, end = "")

. #Hàm tạo đường đi - def createPath(u, v): path = []

j = v

path.append(j)

while before [vertices.index(j)] != u: path.append(before[vertices.index(j)]) before[vertices.index(j)]

j

path.append(u)

path.reverse()

return path

. #Tìm đường đi từ đỉnh u đến đỉnh v trong đồ thị dùng BFS . #Hàm tìm đường đi giữa u và v sử dụng BFS

def findPathBFS (graph, u, v): queue initQueue() enqueue(queue, u)

#Khởi tạo hàng đợi queue

#Thêm đỉnh u vào queue và đánh dấu đã duyệt

visited [vertices.index(u)] = True

#Lập cho đến khi queue rỗng

while not isEmptyQueue(queue):

p dequeue (queue)

“Nếu đỉnh kể với p là v thì trả kết quả đường đi từ u đến v. Ngược lại, Em các đỉnh kề với p vào queue

for neighbor in graph[p]:

if neighbor == V:

before[vertices. index (neighbor)] = p return createPath(u, v)

elif not visited[vertices.index(neighbor)]: visited[vertices.index (neighbor)] = True enqueue(queue, neighbor)

before[vertices. index (neighbor)] = p

#Nếu không tìm thấy đường đi từ u đến v, trả về None. if before[vertices.index(v)] = -1:

return None

- #Hàm tìm đường đi từ đỉnh u đến đỉnh v def findPath(graph, u, v):

 if not u in graph: print("Không có đỉnh",u)

Return đánh", ngời sáng tạo

elif not v in graph: print("Không có đỉnh ", v)

return

global visited, before

visited [False] * len(graph) before = [-1] * len(graph)

path = findPathBFS (graph, u, v) return path

graph, vertices = createAdjListGraph('dothi.txt') #Tạo đồ thị dạng danh sách kề từ tập

u, v = list(map(str, input().split()))

path findPath(graph, u, v)

print(path)

printPath(path, u, v)

Kết quả:

Sử dụng thuật toán duyệt đồ thị theo chiều sâu để tiến hành duyệt tất cả các đỉnh mà u có thể liên kết tới trong đồ thị. Em xây dựng mảng một chiều before với giá trị mặc định của các phần tử là –1 để lưu lại các đỉnh trong quá trình duyệt với quy ước: before[i] = j nghĩa là duyệt đỉnh j trước rồi duyệt đến đỉnh i

def initStack(): return []

def isEmptyStack(stack): return len(stack) == 0 def push(stack, val): stack.append(val) def pop(stack):

return stack.pop() def top(stack):

return stack[len(stack).

ack Rentstack)-Thi sáng tạo

#Tìm đường đi từ đỉnh u đến đỉnh v trong đồ thị dùng DFS #Hàm tìm đường đi giữa u và v sử dụng DFS

def findPathDFS (graph, u, v):

stack = initStack() #Khởi tạo ngăn xếp stack

push(stack, u) #Thêm đỉnh ũ vào stack và đánh dấu đã duyệt visited [vertices.index(u)] = True

#Lập cho đến khi stack rằng while not isEmptyStack(stack): p = top(stack)

found = False

for neighbor in graph[p]:

if not visited[vertices.index(neighbor)]: found = True

break

if found:

visited [vertices.index(neighbor)] = True before [vertices.index(neighbor)] = p if neighbor V:

return createPath(u, v)

else:

else:

push(stack, neighbor)

p = pop(stack)

#Nếu không tìm thấy đường đi từ u đến v, if before[vertices.index(v)] == -1: return None

#Hàm tìm đường đi từ đỉnh u đến đỉnh v def findPath(graph, u, v):

if not u in graph:

print("Không có đỉnh", u)

return

elif not v in graph:

print("Không có đỉnh ", v)

return

global visited, before

visited [False] * len(graph) before [-1] * len(graph)

=

=

path findPathDFS (graph, u, v) return path

#ví dụ minh hoạ

trả về None.

graph, vertices = createAdjListGraph('dothi.txt') #Tạo đồ thị dạng danh sách kề từ tập

u, v

list(map(str, input().split()))

path findPath(graph, u, v)

print (path)

printPath(path, u, v)

Kết quả:

Thuật toán duyệt đô thị theo chiều rộng:

#Duyệt đồ thị G bắt đầu từ đỉnh u def bft (G, u):

đại anh từ trời sáng tạo

Tạo hàng đợi 2 rỗng

Đánh dấu đỉnh u đã duyệt Thêm đỉnh u vào hàng đợi Q while hàng đợi Q khác rỗng: Lấy đính u từ hàng đợi Q xử lí đỉnh

#Thêm các đỉnh kề v của đỉnh u vào hàng đợi a for đỉnh v thuộc tập đỉnh kề của đỉnh u:

if đỉnh v chưa duyệt:

Đánh dấu đỉnh v đã duyệt

Thêm đỉnh v vào hàng đợi Q

Khi đó, thủ tục thực hiện duyệt đồ thị G = (V, E) theo chiều rộng như sau:

#Duyệt đồ thị G theo chiều rộng

 def bfs (G):

#Đánh dấu các đỉnh của đồ thị G chưa duyệt

for đỉnh u thuộc đô thị G:

Đánh dấu đỉnh u chưa duyệt

#Duyệt các đỉnh của đồ thị G for đỉnh u thuộc của đô thị 6: if đỉnh u chưa duyệt:

bft (G, u)

def dfs(G, u):

Xử lí đỉnh u

Đánh dấu duyệt đỉnh u

for đỉnh v là đỉnh kế của đỉnh u:

if đỉnh v chưa được đánh dấu duyệt: dfs(G, v)

Thuật toán duyệt đô thị theo chiều sâu bắt đầu từ đỉnh u:

def dft(G, u):

Khởi tạo ngăn xếp stack rỗng

Xử lí đỉnh u

Đánh dấu duyệt đỉnh u

Thêm đỉnh u vào ngăn xếp stack while ngăn xếp stack khác rỗng:

Xem đỉnh p ở đầu ngăn xếp stack

#Xét các đỉnh kề v chưa được duyệt của đình p found False

for đỉnh v thuộc tập đỉnh kề của đỉnh p: if đỉnh v chưa duyệt:

found=True break

if not found:

Lấy đỉnh p ra khỏi ngăn xếp stack

else:

Xử lí đỉnh v

Đánh dấu duyệt đỉnh v

Thêm đỉnh v vào ngăn xếp stack

Thuật toán duyệt theo chiều sâu các đỉnh của đô thị G được minh hoạ như sau:

def dfs(G):

for đỉnh u thuộc G.

Đánh dấu đỉnh u chưa duyệt.

For đỉnh u thuộc G.

If đỉnh u chưa duyệt

Dft(G,u)