Chuyên đề Tin Học 11 KNTT Bài 11. Bài toán tìm kiếm theo kĩ thuật duyệt có đáp án

Các bài toán tìm kiếm có thể được giải quyết bằng cách sử dụng kĩ thuật duyệt. Kĩ thuật duyệt là lần lượt kiểm tra các phân tử trong miền tim kiếm để xác định xem phần tử đó có thoả mãn điều kiện tìm kiếm hay không. Tuy vào yêu cầu tìm kiếm, miền tìm kiếm mà kĩ thuật duyệt có thể được thiết kế theo các cách khác nhau.

a) Trong yêu cầu a, chỉ cần tìm một học sinh có điểm Toán lớn hơn điểm Vật lí nên có thể thực hiện tìm kiếm duyệt tuần tự từ học sinh đầu tiên trong dãy. Khi gặp học sinh có điểm Toán không lớn hơn điểm Vật lí thi tiếp tục duyệt học sinh tiếp theo. Khi gặp học sinh đầu tiên có điểm Toán lớn hơn điểm Vật lí thì dừng chương trình và in tên học sinh đó lên màn hình.

        b) Trong yêu cầu b, cần tìm tất cả các học sinh có điểm Vật lí lớn hơn điểm Hoá học. Như vậy, ta cần duyệt tất cả các học sinh, ngay cả khi đã tìm thấy một học sinh có điểm Vật lí lớn hơn điểm Hoá học thì chương trình vẫn tiếp tục duyệt đề tìm ra tất cả học sinh thoả mãn điều kiện.

        c) Trong yêu cầu c, do danh sách tên và điểm các môn khác được sắp xếp theo điểm Toán tăng dần nên ta có thể duyệt từ cuối dãy và dùng tìm kiếm khi gặp điểm Toán nhỏ hơn 9.

Yêu cầu a có số vòng lặp nhỏ nhất, chỉ cần tìm được 1 học sinh phù hợp và kết thúc chương trình. Còn ở yêu cầu b, c thì cần duyệt tất cả các học sinh nên số vòng lặp sẽ lớn hơn.

a) Tìm học sinh có điểm Toán bằng 8.9.

Để tìm học sinh có điểm Toán bằng 8.9, ta có thể dùng hàm index() để tìm chỉ số của giá trị trong danh sách B, sau đó lấy tên của học sinh ở vị trí đó trong danh sách A.

b) Tìm một học sinh có tổng điểm ba môn Toán, Vật lí, Hoá học lớn hơn 26.5.

Để tìm một học sinh có tổng điểm ba môn Toán, Vật lí, Hoá học lớn hơn 26.5, ta có thể dùng vòng lặp for để duyệt qua danh sách điểm của từng học sinh và tính tổng điểm của ba môn. Nếu tổng lớn hơn 26.5 thì lấy tên của học sinh đó ở vị trí tương ứng trong danh sách A.

c) Tìm học sinh có tổng điểm ba môn Toán, Vật lí, Hoá học nhỏ nhất.

Để tìm học sinh có tổng điểm ba môn Toán, Vật lí, Hoá học nhỏ nhất, ta sẽ ghép các danh sách điểm thành một danh sách con, sau đó tính tổng điểm của từng học sinh và lấy tên học sinh có tổng điểm nhỏ nhất.

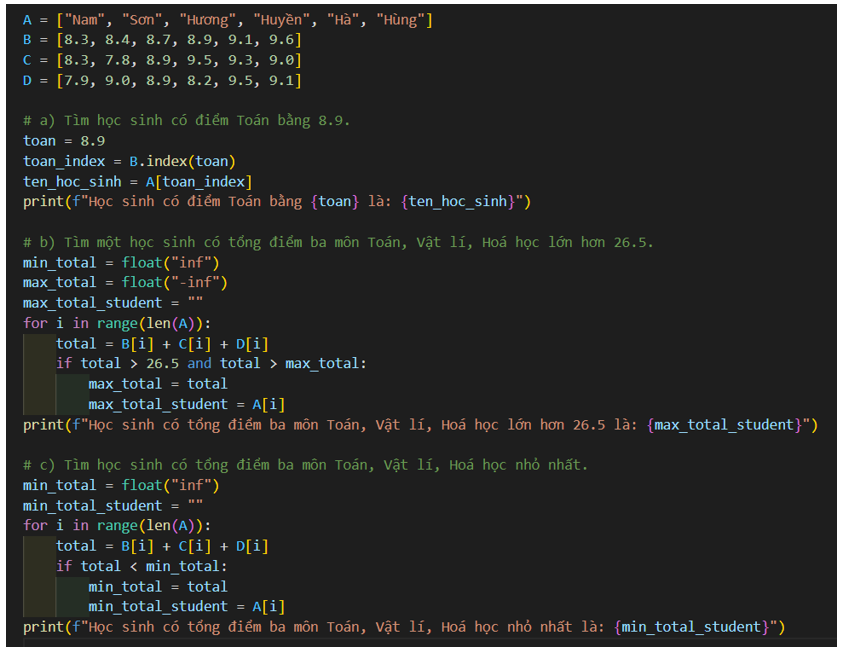
Kết quả là

1. Để giải quyết bài toán tìm tất cả các xâu nhị phân có độ dài n, ta có thể sử dụng kỹ thuật duyệt vét cạn trên mảng một chiều có độ dài n. Với mỗi phần tử trong mảng, ta sẽ thử đặt giá trị 0 hoặc 1 vào đó và tiếp tục thử đặt giá trị cho các phần tử tiếp theo. Khi đã duyệt hết tất cả các phần tử trong mảng, ta sẽ có được một xâu nhị phân độ dài n. Quá trình này sẽ được lặp lại cho đến khi tất cả các xâu nhị phân độ dài n đã được tìm thấy.

        2. Để giải quyết bài toán tìm tất cả các hoán vị của tập hợp [1, 2, ..., n], ta có thể sử dụng kỹ thuật đệ quy. Với mỗi số trong tập hợp [1, 2, ..., n], ta đưa số đó vào một mảng và gọi lại hàm đệ quy với tập hợp [1, 2, ..., n] đã loại bỏ số đó. Quá trình đệ quy sẽ được tiếp tục cho đến khi tất cả các số đã được sử dụng trong mảng, lúc đó ta sẽ có được một hoán vị của tập hợp [1, 2, ..., n]. Quá trình này sẽ được lặp lại cho đến khi tất cả các hoán vị của tập hợp [1, 2, ..., n] đã được tìm thấy.