Đề ôn luyện Toán Chương 1. Ứng dụng đạo hàm để khảo sát hàm số (đề số 1)
38 người thi tuần này 4.6 1.4 K lượt thi 22 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
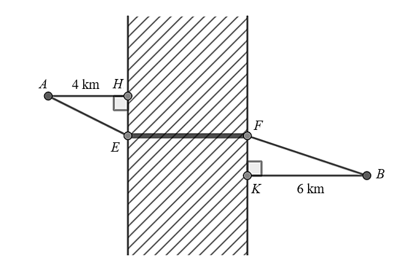
Câu 1
D. \(\left( { - 1;\,1} \right)\)
Lời giải
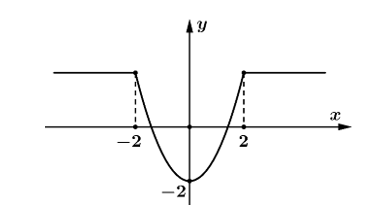
Quan sát đồ thị, ta thấy hàm số đồng biến trên khoảng \(\left( { - 1;\,1} \right)\). Chọn D.
Câu 2
A. \(4\).
B. \(2\).
C. \(0\).
D. \(1\).
Lời giải
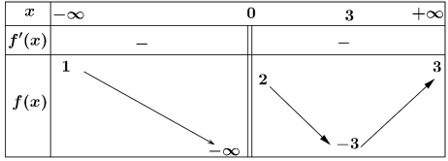
Dựa vào bảng biến thiên, ta có giá trị cực tiểu của hàm số đã cho bằng \(0\). Chọn C.
Câu 3
A. \[\left( {2;3} \right)\]
B. \[\left( { - 1;1} \right)\]
C. \[\left( {0;2} \right)\]
D. \[\left( { - \infty ;1} \right)\].
Lời giải
Ta có \(f'\left( x \right) = {x^2}\left( {x + 2} \right)\left( {1 - x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = - 2\end{array} \right.\).
Bảng biến thiên:
![Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\)và có \(f'\left( x \right) = {x^2}\left( {x + 2} \right)\left( {1 - x} \right),\,\forall x \in \mathbb{R}\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/screenshot-2025-11-04-082404-1762219341.png)
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng \(\left( {1; + \infty } \right) \supset \left( {2;3} \right)\). Chọn A.
Câu 4
A. \(3\)
B. \(2\)
C. \(1\)
D. \(4\).
Lời giải
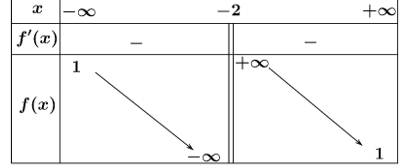
Ta có \[M = \mathop {{\rm{max}}}\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( { - 1} \right) = 3\] và \(m = \mathop {{\rm{min}}}\limits_{\left[ { - 1;2} \right]} \,f\left( x \right) = f\left( 0 \right) = 0\).
Vậy \(M + m = 3\). Chọn A.
Câu 5
A. \(y = - \frac{1}{5}\)
B. \(x = - \frac{1}{5}\)
C. \(y = - \frac{2}{5}\)
D. \(x = - \frac{2}{5}\).
Lời giải
Xét hàm số \(y = \frac{{ - 2x + 3}}{{5x + 1}}\).
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{5}} \right\}\).
Ta có .
Vậy đường thẳng \(x = - \frac{1}{5}\) là tiệm cận đứng của đồ thị hàm số \(y = \frac{{ - 2x + 3}}{{5x + 1}}\). Chọn B.
Lưu ý: Đối với hàm số phân thức bậc nhất chia bậc nhất \(y = \frac{{ax + b}}{{cx + d}}\) \(\left( {a \ne 0,c \ne 0,ad - bc \ne 0} \right)\) thì ta có thể kết luận ngay đồ thị hàm số này có tiệm cận đứng là \(x = - \frac{d}{c}\) và tiệm cận ngang là \(y = \frac{a}{c}\). Như vậy, trong bài tập trên ta có thể chọn ngay phương án B mà không cần tính giới hạn.
Câu 6
D. \[ - 1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(y = {x^3} - 3{x^2} + 1\).
B. \(y = \frac{{x - 1}}{{x + 1}}\)
C. \(y = \frac{{x + 2}}{{x + 1}}\)
D. \(y = - {x^4} + 2{x^2} + 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(y = - 2\)
B. \(y = 1\).
B. \(y = 1\).
D. \(y = x\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(x = - 2\).
B. \(x = 0\).
C. \(\left( { - 2\,;\, - 2} \right)\).
D. \(\left( {0\,;\, - 2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \( - 1\).
B. \(4\).
C. \(1\).
D. \(2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \[3\].
B. \[1\].
C. \[2\].
D. \[0\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
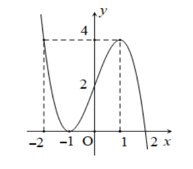
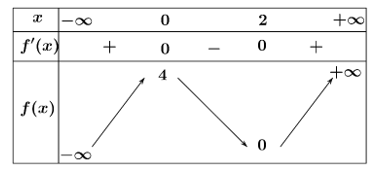
![Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 3;2} \right]\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/screenshot-2025-11-04-082626-1762219471.png)
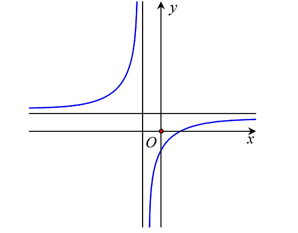
![Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/blobid1-1762220427.png)