15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 11: Định lí và chứng minh định lý có đáp án
77 người thi tuần này 4.6 1.8 K lượt thi 15 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu Trắc nghiệm Toán 7 Cánh Diều Ôn tập chương I (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 7 Cánh Diều Bài 5. Biểu diễn thập phân của số hữu tỉ (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 7 Cánh Diều Bài 4. Thứ tự thực hiện phép tính. Quy tắc dấu ngoặc (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 7 Cánh Diều Bài 3. Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 7 Cánh Diều Bài 2. Cộng, trừ, nhân, chia số hữu tỉ (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 7 Cánh Diều Bài 1. Tập hợp Q các số hữu tỉ (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 7 Kết nối tri thức Ôn tập Chương II (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 7. Tập hợp các số thực (Đúng sai - Trả lời ngắn) có đáp án
Danh sách câu hỏi:
Câu 1
A. một khẳng định được suy ra từ những khẳng định đúng đã biết;
B. một khẳng định được suy ra từ những khẳng định không đúng đã biết;
C. một tính chất được suy ra từ những khẳng định đúng;
D. một tính chất được suy ra từ những khẳng định chưa biết.
Lời giải
Đáp án đúng là: A
Định lý là một khẳng định được suy ra từ những khẳng định đúng đã biết.
Câu 2
A. Thì … là…;
B. Do … nên …,
C. Vì … nên …;
D. Nếu … thì ….
Lời giải
Đáp án đúng là: D
Mỗi định lí thường được phát biểu dưới dạng “Nếu … thì …”.
Câu 3
A. Giả thiết là “hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba”;
B. Giả thiết là “chúng song song với nhau”;
C. Giả thiết là “hai đường thẳng phân biệt cùng song song với một đường thứ ba thì chúng song song với nhau”;
D. Giả thiết là “hai đường thẳng phân biệt cùng song song”.
Lời giải
Đáp án đúng là: A.
Giả thiết là vế đứng trước “thì”.
Do đó giả thiết là “hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba”.
Vậy chọn đáp án A.
Câu 4
A. Giả thiết của định lí là điều cho biết;
B. Kết luận của định lí là điều suy ra;
C. Giả thiết của định lí là điều suy ra;
D. Cả A và B đều đúng.
Lời giải
Đáp án đúng là: C
Giả thiết của định lí là phần cho biết. Kết luận của định lí là điều suy ra.
Vậy chọn đáp án C.
Câu 5
A. M thuộc AB;
B. M không thuộc AB và cách đều A, B;
C. M thuộc AB và cách đều A, B;
D. M không thuộc AB.
Lời giải
Đáp án đúng là: C
Nếu M là trung điểm của đoạn thẳng AB thì M là điểm thuộc AB và cách đều A, B.
Vậy chọn đáp án C.
Câu 6
A. \[\widehat {aOt} = \widehat {tOb}\];
B. \[\widehat {aOb} = \widehat {tOb}\];
C. \[\widehat {aOt} = \frac{1}{2}\widehat {aOb}\];
D. Đáp án A và C đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Hai góc kề bù bằng nhau;
B. Hai góc so le trong bằng nhau;
C. Hai góc trong cùng phía bằng nhau;
D. Hai góc kề nhau bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
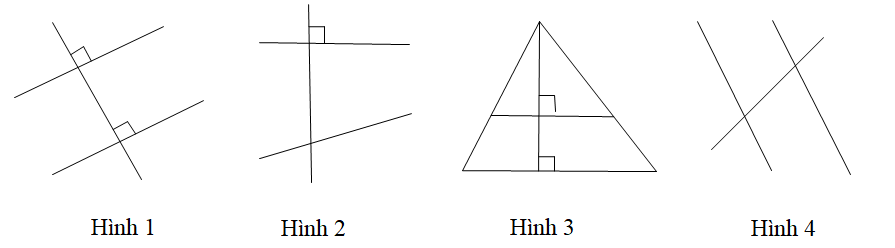
Câu 8
A. Hình 1, Hình 2;
B. Hình 2, Hình 3;
C. Hình 3, Hình 4;
D. Hình 1, Hình 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
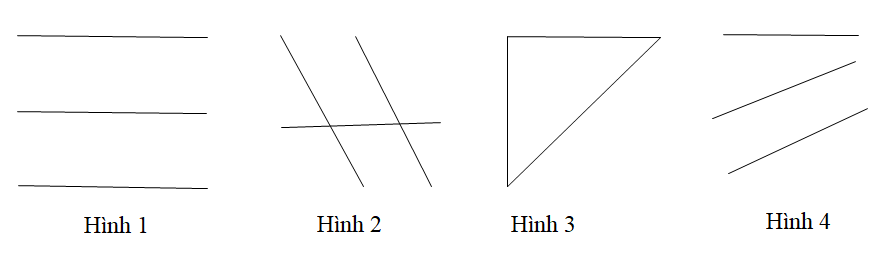
Câu 9
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. hai góc đó có tổng số đo bằng 180°;
B. hai góc đó có tổng số đo bằng 90o;
C. hai góc đó bằng nhau;
D. hai góc đó không bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. giả thiết;
B. trả lời;
C. ý nghĩa;
D. định nghĩa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Phát biểu định lí sau bằng lời.
|
Giả thiết |
t cắt m tại A, t cắt n tại B \[\widehat {{A_1}}\] và \[\widehat {{B_1}}\]là hai góc đồng vị \[\widehat {{A_1}} = \widehat {{B_1}}\] |
|
Kết luận |
m // n |
A. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n vuông góc với nhau;
B. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n song song với nhau;
C. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n song song với nhau;
D. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n vuông góc với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
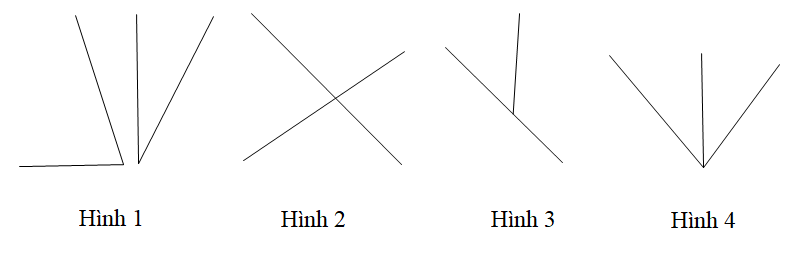
Câu 13
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
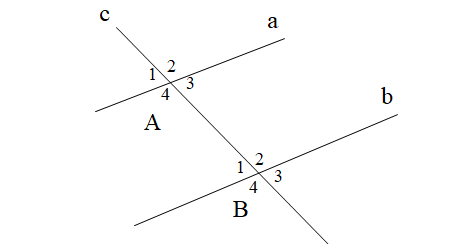
Câu 14
A.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_4}}\] và \[\widehat {{B_2}}\] là hai góc so le trong \[\widehat {{A_4}} = \widehat {{B_2}}\] |
|
Kết luận |
a // b |
B.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đối đỉnh \[\widehat {{A_3}} = \widehat {{B_1}}\] |
|
Kết luận |
a // b |
C.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc so le trong \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
|
Kết luận |
a // b |
D.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đồng vị \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
|
Kết luận |
a // b |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. kết luận;
B. khẳng định;
C. chứng minh;
D. Cả 3 đáp án đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.