Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:
a) AI < (AB + AC);
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:
a) AI < (AB + AC);
Câu hỏi trong đề: Bài tập Bài tập cuối chương 9 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
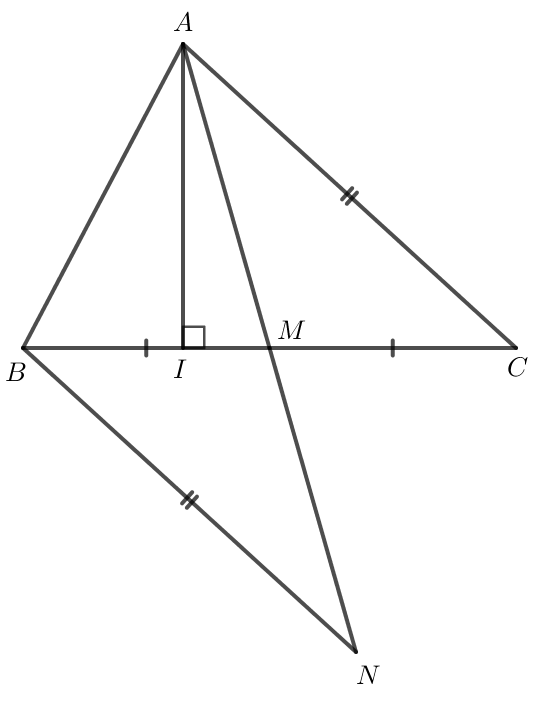
a)
vuông tại I nên AC là cạnh huyền.
Do đó AC > AI (1).
vuông tại I nên AB là cạnh huyền.
Do đó AB > AI (2).
Từ (1) và (2) ta có AB + AC > AI + Ai hay AB + AC > 2AI
Suy ra AI <
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đổi 1,2 m = 120 cm.
Chúng ta có các trường hợp sau:
Trường hợp 1. Cạnh dài 30 cm là cạnh đáy của tam giác cân.
Khi đó độ dài 2 cạnh bên là: (120 - 30) : 2 = 45 cm.
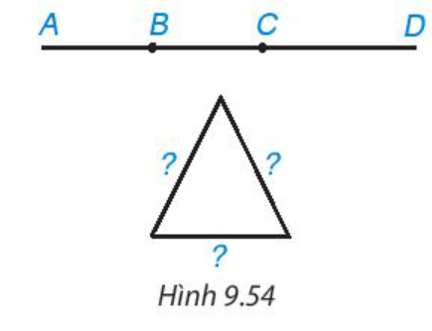
Vậy để gấp được tam giác có ba cạnh dài 30 cm, 45 cm, 45 cm, ta đánh dấu hai điểm ở giữa hai đầu mút đoạn dây, chia đoạn dây thành ba đoạn thẳng có độ dài 30 cm, 45 cm, 45 cm, trong đó đoạn dài 30 cm chứa một mút hoặc không chứa mút nào của đoạn dây như hình vẽ dưới đây.
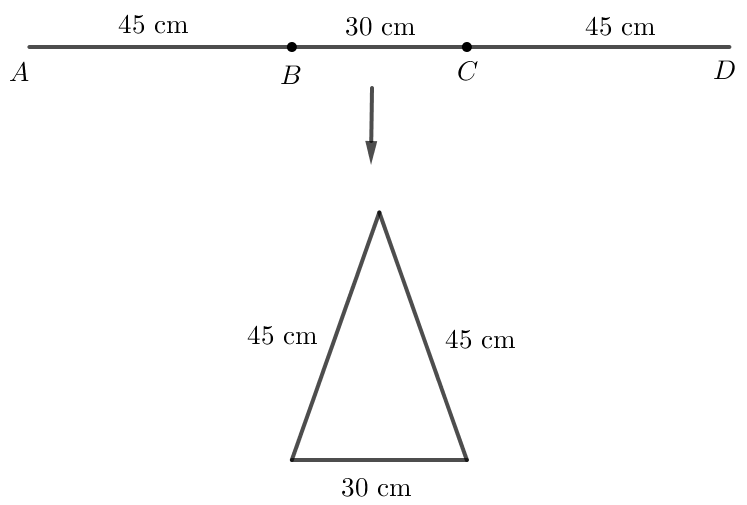
Trường hợp 2. Cạnh dài 30 cm là cạnh bên của tam giác cân.
Khi đó độ dài cạnh đáy là: 120 - 30 - 30 = 60 cm.
Ta thấy 30 + 30 = 60 nên bộ ba đoạn thẳng có độ dài 30 cm, 30 cm, 60 cm không thể tạo thành một tam giác.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
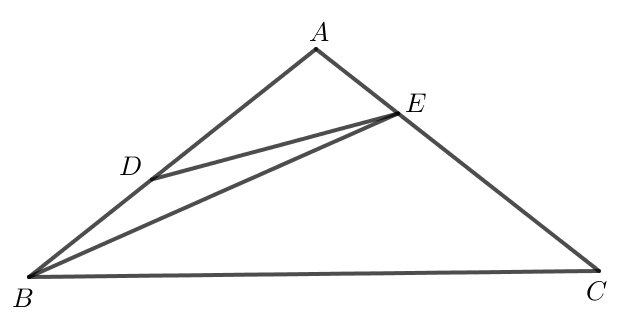
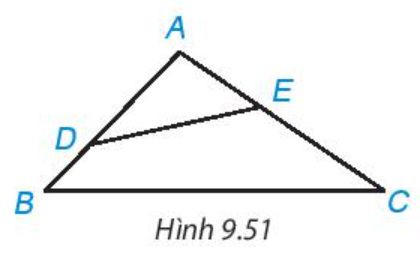
Xét tam giác ADE có là góc ngoài của đỉnh D nên
Mà là góc tù nên là góc tù.
Xét tam giác BDE có:
là góc tù nên là góc lớn nhất trong tam giác. Do đó, BE > DE (1)
Xét tam giác ABE có là góc ngoài của đỉnh E nên
Mà là góc tù nên là góc tù.
Xét tam giác BEC có:
là góc tù nên là góc lớn nhất trong tam giác. Do đó, BC > BE (2)
Từ (1) và (2) suy ra, BC > DE (điều phải chứng minh).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập
Minh Khôi Nguyễn
phần b đâu