Câu hỏi:

19/08/2025 3,069

Cho tam giác vuông với các cạnh góc vuông có độ dài là 3 cm và 4 cm , kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng mà nó chia ra trên cạnh huyền.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 1: Hệ thức lượng trong tam giác vuông có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

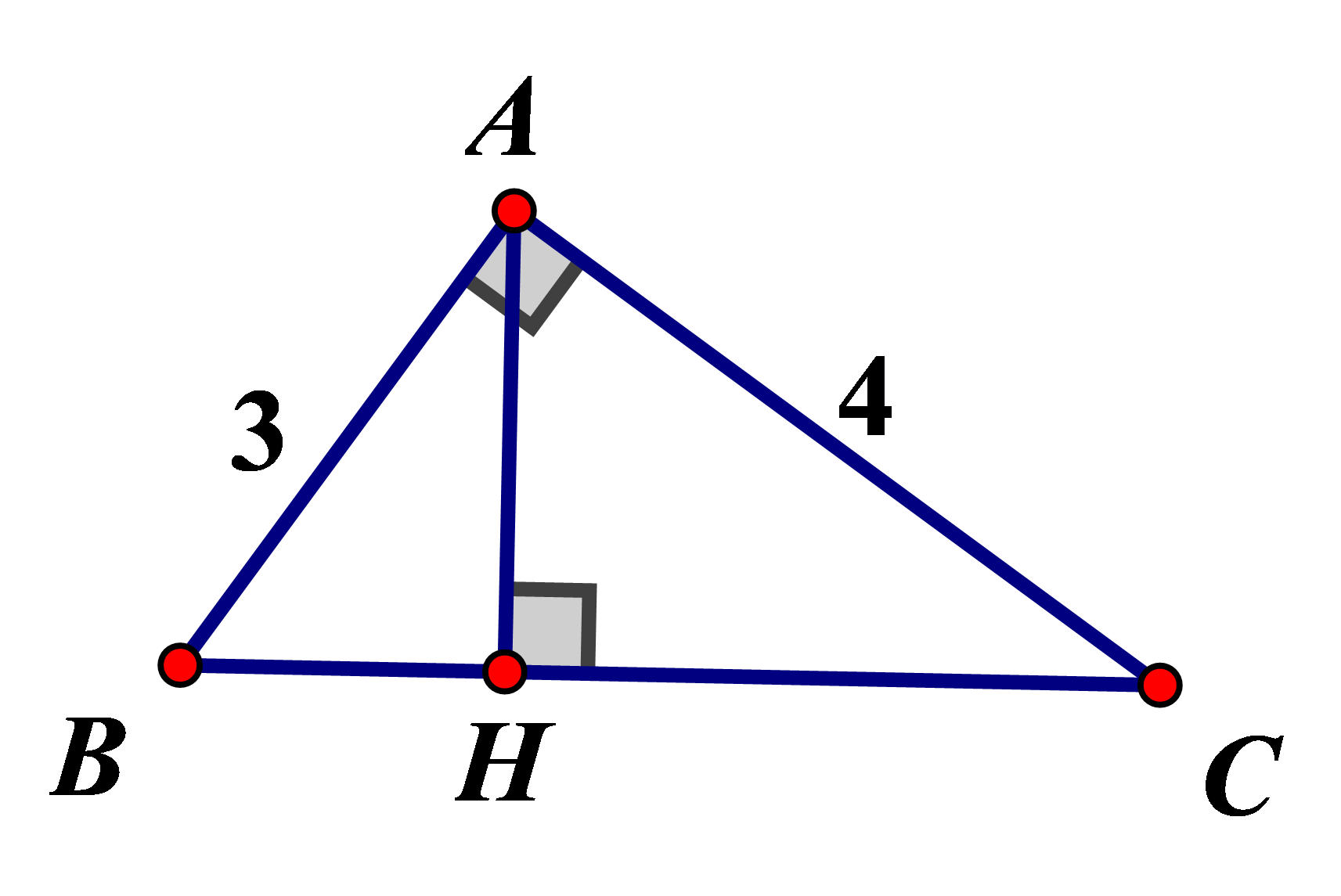
Media VietJack

Giả sử tam giác ABC có các cạnh góc vuông AB = 3cm, AC = 4cm, AH là đường cao.

Áp dụng định lí Pitago cho tam giác vuông ABC:

$B C^{2} = A B^{2} + A C^{2} = 3^{2} + 4^{2} = 25 \Rightarrow B C = 5$ cm

Áp dụng hệ thức lượng trong tam giác vuông ta có:

$B A^{2} = B H . B C \Rightarrow B H = \frac{B A^{2}}{B C} \Rightarrow B H = \frac{3^{2}}{5} \Rightarrow B H = \frac{9}{5}$ (cm)

$C A^{2} = C H . C B \Rightarrow C H = \frac{C A^{2}}{C B} \Rightarrow C H = \frac{4^{2}}{5} \Rightarrow C H = \frac{16}{5}$ (cm)

$A H^{2} = H B . H C \Rightarrow A H^{2} = \frac{9}{5} . \frac{16}{5} \Rightarrow A H = \frac{12}{5}$ (cm)

(Có thể tính đường cao AH bởi công thức $\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$ )

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

(Hãy giải bằng nhiều cách khác nhau)

Cho tam giác ABC vuông tại A, AH là đường cao. Biết AB=8cm, AC=6cm. Tính độ dài AH.

Xem đáp án

Lời giải

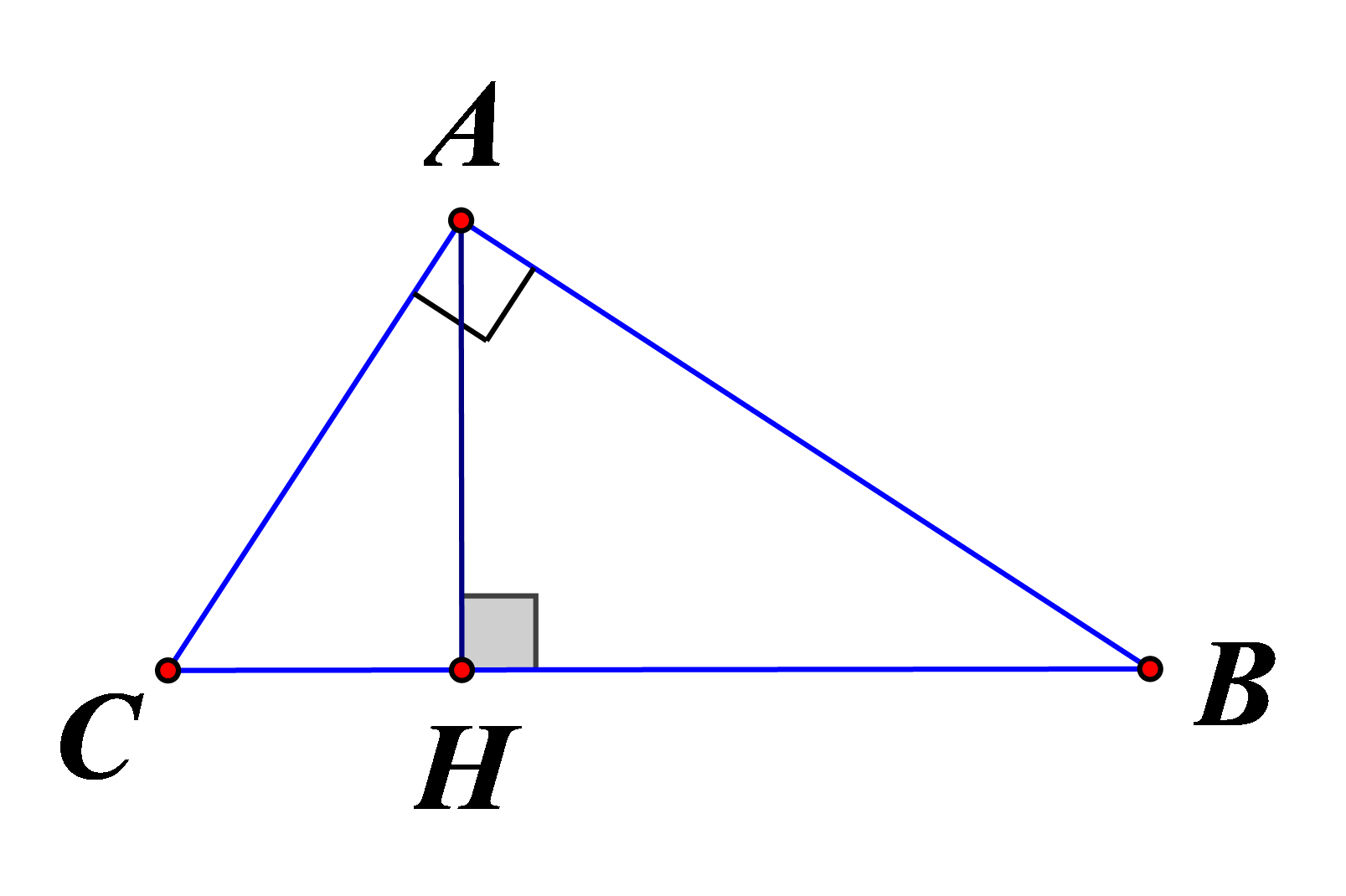
*Cách 1: Ta có $Δ A B C$ vuông tại A nên :

$B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{8^{2} + 6^{2}} = 10 (c m)$ (Định lý Pytago)

$Δ A B C$ vuông tại A, AH $⊥$ BC, nên $A H . B C = A B . A C \Rightarrow A H = \frac{A B . A C}{B C} = 4, 8 (c m)$

*Cách 2: $Δ A B C$ vuông tại A, AH $⊥$ BC, nên: $\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}} \Rightarrow A H^{2} = \frac{A B^{2} . A C^{2}}{A B^{2} + A C^{2}} \Rightarrow A H = \sqrt{\frac{64.36}{100}} = 4.8 (c m)$

*Cách 3: Tam giác ABC vuông tại A, Theo định lý Pytago ta có

$B C^{2} = A B^{2} + A C^{2} = 8^{2} + 6^{2} = 100$ nên suy ra BC=10cm.

$Δ A B C$ vuông tại A nên: $B H . B C = A B^{2} \Rightarrow B H = \frac{A B^{2}}{B C} = 6.4 (c m)$ . Mà $H C = B C - B H = 3, 6$ (cm)

$Δ A B C$ vuông tại A, AH $⊥$ BC, nên: $A H^{2} = B H . H C = {4.8}^{2} \Rightarrow A H = 4.8 (c m)$

*Cách 4:

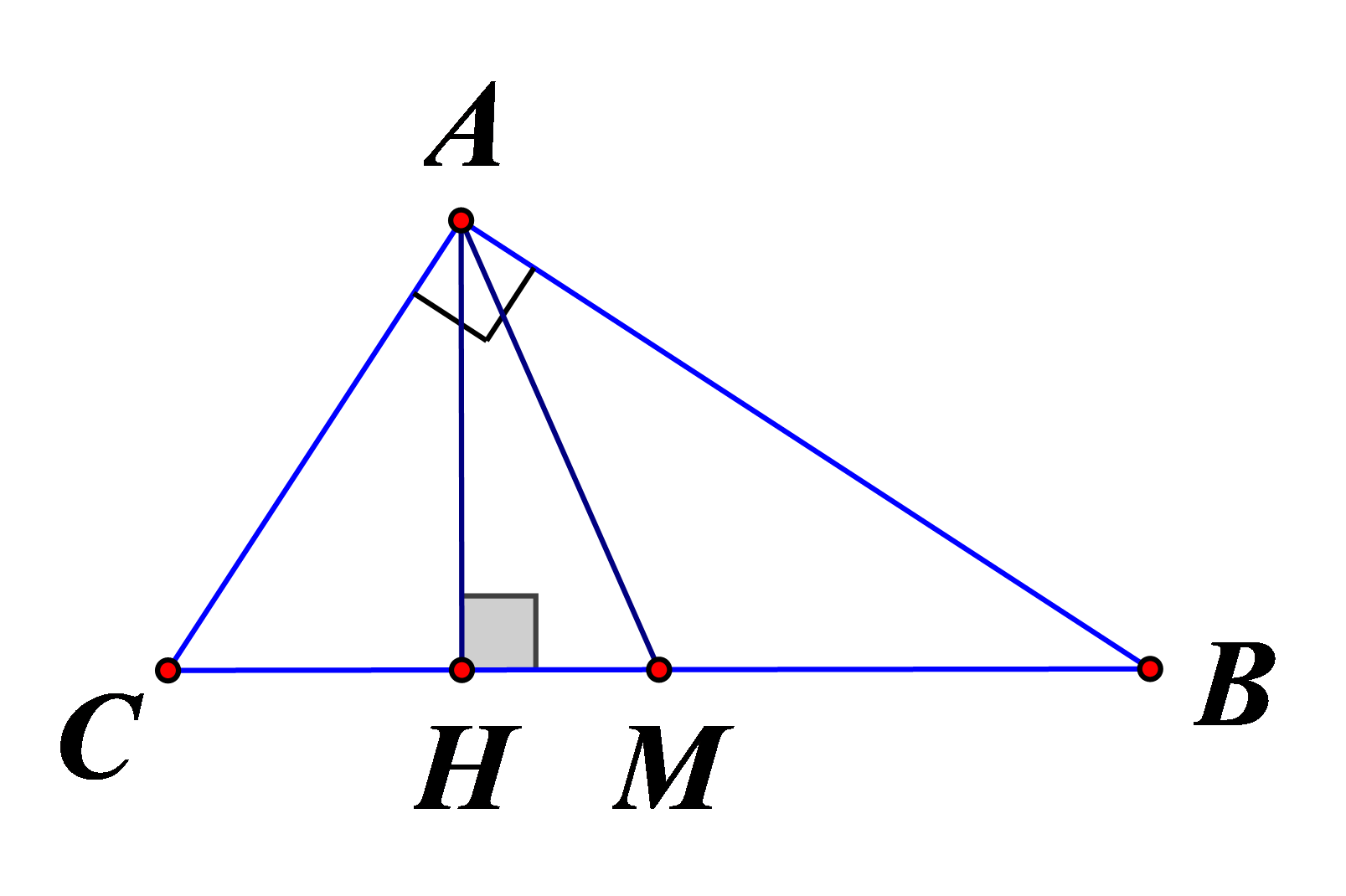
Media VietJack

Gọi M là trung điểm BC.

Ta có : $B M = A M = \frac{1}{2} B C = 5 c m$

+ Tính được BH=6.4cm

+ Nên $M H = B H - B M = 6, 4 - 5 = 1 (c m)$

Áp dụng định lý Pitago vào $Δ H A M$ vuông tại H: $A H = \sqrt{A M^{2} - M H^{2}} = \sqrt{5^{2} - 1, 4^{2}} = 4, 8 (c m)$

Câu 2

Cho tam giác ABC cân tại A. Các tia phân giác của góc A và góc B cắt nhau tại O. Biết $OA = 2 \sqrt{3}$ cm, OB = 2cm, tính độ dài AB.

Xem đáp án

Lời giải

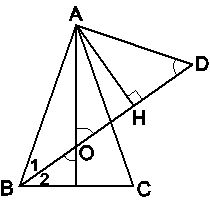
Media VietJack

Qua A vẽ một đường thẳng vuông góc với AB cắt tia BO tại D.

Ta có $\hat{D} + \hat{B_{1}} = 90^{°}$

mà $\hat{B_{1}} = \hat{B_{2}}$ nên $\hat{A O D} = \hat{D}$

Do đó DAOD cân tại A. Suy ra $A D = A O = 2 \sqrt{3}$ (cm).

Vẽ AH ^ OD thì HO = HD.

Ta đặt $H O = H D = x$ thì $B D = 2 x + 2.$

Xét DABD vuông tại A, đường cao AH, ta có $A D^{2} = B D . H D .$

Suy ra ${(2 \sqrt{3})}^{2} = x (2 x + 2)$ Từ đó ta được phương trình:

$2 x^{2} + 2 x - 12 = 0$ Û (x – 2)(x + 3) = 0 Û x = 2 hoặc x = -3.

Giá trị x = 2 được chọn, giá trị x = -3 bị loại.

Do đó $B D = 2 + 2 + 2 = 6$ (cm). Suy ra $A B = \sqrt{6^{2} - {(2 \sqrt{3})}^{2}} = \sqrt{24} = 2 \sqrt{6}$ (cm).

Câu 3

Cho hình vuông ABCD cạnh 1. Gọi M là một điểm nằm giữa B và C. Tia AM cắt đường thẳng CD tại N. Tính giá trị của biểu thức $P = \frac{1}{{AM}^{2}} + \frac{1}{{AN}^{2}}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC vuông tại A, BC = 20cm. Biết tỉ số hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là 9 : 16. Tính diện tích tam giác ABC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình thang ABCD, $\hat{A} = \hat{D} = 90^{°} =$ hai đường chéo vuông góc với nhau tại O. Cho biết AD = 12cm; CD = 16cm. Tính các độ dài OA, OB, OC, OD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho tam giác ABC cân tại A có các đường cao AH và BK. Chứng minh rằng : $\frac{1}{B K^{2}} = \frac{1}{B C^{2}} + \frac{1}{4 A H^{2}}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

(Hãy giải bằng nhiều cách khác nhau)

Cho tam giác ABC vuông tại A, AH là đường cao. Biết AB=8cm, AC=6cm. Tính độ dài AH.

Cho tam giác ABC cân tại A. Các tia phân giác của góc A và góc B cắt nhau tại O. Biết $OA = 2 \sqrt{3}$ cm, OB = 2cm, tính độ dài AB.

Cho hình vuông ABCD cạnh 1. Gọi M là một điểm nằm giữa B và C. Tia AM cắt đường thẳng CD tại N. Tính giá trị của biểu thức $P = \frac{1}{{AM}^{2}} + \frac{1}{{AN}^{2}}$

Cho hình thang ABCD, $\hat{A} = \hat{D} = 90^{°} =$ hai đường chéo vuông góc với nhau tại O. Cho biết AD = 12cm; CD = 16cm. Tính các độ dài OA, OB, OC, OD.

Cho tam giác ABC cân tại A có các đường cao AH và BK. Chứng minh rằng : $\frac{1}{B K^{2}} = \frac{1}{B C^{2}} + \frac{1}{4 A H^{2}}$