Tìm góc x, biết rằng:sinx+cosx=2

Bình phương hai vế ta được: sin2x + 2sin x.cos x + cos2x = 2 2sin x.cos x + 1 = 2(vì sin2x + cos2x = 1) 2sin x.cos x = 1Û 1 – 2sin x.cos x = 0 Û sin2x − 2sin x.cos x + cos2x=0 sin x – cos x2= 0. Do đó sin x = cos x sin x = sin (90o– x) (vì cos x = sin (90o– x) ) Dẫn tới x = 90o– x⇔2x = 90o⇔x = 45o. Nhận xét: Phương pháp chung để giải ví dụ này là tìm cách đưa phương trình có hai tỉ số lượng giác về dạng còn một tỉ số lượng giác bằng cách vận dụng quan hệ giữa các tỉ số lượng giác đó

Câu hỏi:

12/07/2024 724

Tìm góc x, biết rằng: $\sin x + \cos x = \sqrt{2}$

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 1: Hệ thức lượng trong tam giác vuông có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Bình phương hai vế ta được: $s i n^{2} x + 2 s i n x . c o s x + c o s^{2} x = 2$

$2 s i n x . c o s x + 1 = 2$ (vì $s i n^{2} x + c o s^{2} x = 1$ )

$2 s i n x . c o s x = 1$ Û $1 - 2 s i n x . c o s x = 0$ Û $s i n^{2} x - 2 s i n x . c o s x + c o s^{2} x = 0$

${(s i n x - c o s x)}^{2} = 0$ . Do đó $s i n x = c o s x$

$s i n x = s i n (90^{o} - x)$ (vì $c o s x = s i n (90^{o} - x)$ )

Dẫn tới $x = 90^{o} - x \Leftrightarrow 2 x = 90^{o} \Leftrightarrow x = 45^{o} .$

Nhận xét: Phương pháp chung để giải ví dụ này là tìm cách đưa phương trình có hai tỉ số lượng giác về dạng còn một tỉ số lượng giác bằng cách vận dụng quan hệ giữa các tỉ số lượng giác đó

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chứng minh định lí sin: Trong một tam giác nhọn, độ dài các cạnh tỉ lệ với sin của các góc đối diện: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Xem đáp án

Lời giải

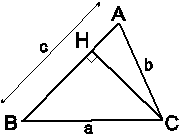
Media VietJack

* Tìm cách giải:

Để có sin A (hoặc sin B, sin C) thì phải xét tam giác vuông với A là một góc nhọn. Do đó phải vẽ thêm đường cao.

* Trình bày lời giải:

Vẽ đường cao CH.

Xét DACH vuông tại H ta có: $\sin A = \frac{CH}{AC}$ (1)

Xét DBCH vuông tại H ta có: $\sin B = \frac{CH}{BC}$ (2)

Từ (1) và (2) suy ra $\frac{\sin A}{\sin B} = \frac{C H}{A C} : \frac{C H}{B C} = \frac{B C}{A C} = \frac{a}{b}$ . Do đó $\frac{a}{\sin A} = \frac{b}{\sin B}$

Chứng minh tương tự ta được $\frac{b}{\sin B} = \frac{c}{\sin C}$

Vậy $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Lưu ý: Nếu DABC có $\hat{C} \geq 90^{°}$ thì ta vẫn có: $\frac{a}{\sin A} = \frac{b}{\sin B}$

Câu 2

Không dùng máy tính hoặc bảng số, tính giá trị của các biểu thức sau bằng cách hợp lí:

$P = \sin^{2} 1^{°} + \sin^{2} 2^{°} + \sin^{2} 3^{°} + \dots + \sin^{2} 88^{°} + \sin^{2} 89^{°}$

Xem đáp án

Lời giải

Áp dụng định lí nếu hai góc phụ nhau thì sin của góc này bằng côsin góc kia, tang của góc này bằng côtang góc kia, ta có:

$P = \sin^{2} 1^{°} + \sin^{2} 2^{°} + \sin^{2} 3^{°} + \dots + \sin^{2} 88^{°} + \sin^{2} 89^{°}$

$= (\sin^{2} 1^{°} + \sin^{2} 89^{°}) + (\sin^{2} 2^{°} + \sin^{2} 88^{°}) + .... + (\sin^{2} 44^{°} + \sin^{2} 46^{°}) + \sin^{2} 45^{°} = (\sin^{2} 1^{°} + c {os}^{2} 1^{°}) + (\sin^{2} 2^{°} + c {os}^{2} 2^{°}) + .... + (\sin^{2} 44^{°} + c {os}^{2} 44^{°}) + \sin^{2} 45^{°}$

= $1 + 1 + 1 + ... + 1 + {(\frac{\sqrt{2}}{2})}^{2} = 44, 5$

Câu 3