Câu hỏi:
12/07/2024 502
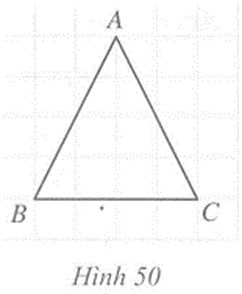
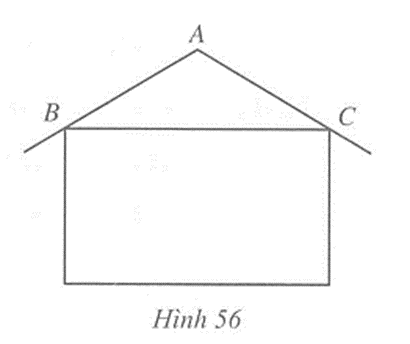
Trong thiết kế của một ngôi nhà độ nghiêng của mái nhà so với phương nằm ngang phải phù hợp với kết cấu của ngôi nhà và vật liệu làm mái nhà. Hình 56 mô tả mặt cắt đứng của ngôi nhà, trong đó độ nghiêng của mái nhà so với phương nằm ngang được biểu diễn bởi số đo góc ở đáy của tam giác ABC cân tại A. Tính độ nghiêng của mái nhà so với phương nằm ngang trong mỗi trường hợp sau:
Góc ở đỉnh A (khoảng) 140o đối với mái nhà lợp bằng fibro xi măng.
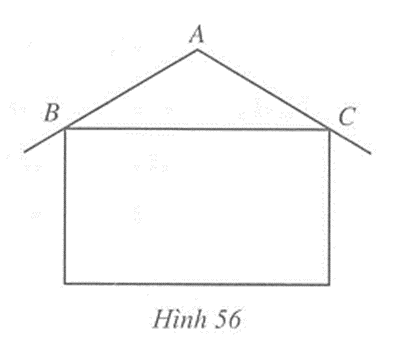
Trong thiết kế của một ngôi nhà độ nghiêng của mái nhà so với phương nằm ngang phải phù hợp với kết cấu của ngôi nhà và vật liệu làm mái nhà. Hình 56 mô tả mặt cắt đứng của ngôi nhà, trong đó độ nghiêng của mái nhà so với phương nằm ngang được biểu diễn bởi số đo góc ở đáy của tam giác ABC cân tại A. Tính độ nghiêng của mái nhà so với phương nằm ngang trong mỗi trường hợp sau:
Góc ở đỉnh A (khoảng) 140o đối với mái nhà lợp bằng fibro xi măng.
Câu hỏi trong đề: Giải VBT Toán 7 Cánh diều Bài 7. Tam giác cân có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tam giác ABC cân tại A nên \(\widehat {ABC}\) = \(\widehat {ACB}\)
Ta có: \(\widehat {ABC}\) + \(\widehat {ACB}\) + \(\widehat A\) = 180° (tổng ba góc của một tam giác).
Suy ra \(\widehat {ABC}\) = \(\widehat {DAC}\)= \(\frac{{18{0^o} - \widehat A}}{2}\)
Với \(\widehat A\) = 140o, ta có \(\widehat {ABC} = \frac{{18{0^o} - {{140}^o}}}{2} = 2{0^o}\).
Độ nghiêng của mái nhà so với phương nằm ngang bằng 20o.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
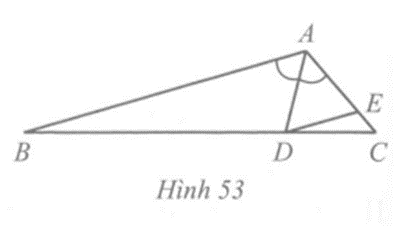
Vì AD là tia phân giác của góc BAC, nên
\(\widehat {BAD}\) = \(\widehat {CAD}\) = \(\frac{1}{2}\)\(\widehat {BAC}\) = 60o
Tức là \(\widehat {DAE}\) = 60°
Ta có DE // AB (giả thiết) nên \(\widehat {ADE}\) = \(\widehat {DAB}\) (hai góc so le trong) do đó \(\widehat {ADE}\) = 60°.
Vậy tam giác ADE có \(\widehat {DAE}\) = \(\widehat {ADE}\) = 60o nên tam giác ADE là tam giác cân và có một góc bằng 60° nên tam giác ADE là tam giác đều.
Lời giải
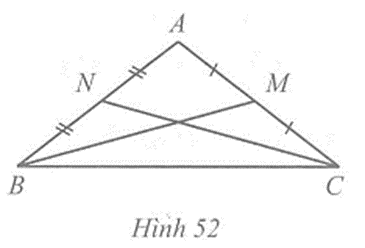
Vì M, N lần lượt là trung điểm của AC và AB nên
AM = \(\frac{1}{2}\) AC, AN = \(\frac{1}{2}\) AB.
Mà AC = AB (vì tam giác ABC cân tại A) nên AM = AN
Xét hai tam giác ABM và ACN, ta có:
AB = AC, \(\widehat A\) là góc chung; AM = AN .
Suy ra ∆ABM = ∆ACN (c.g.c)
Do đó BM = CN (hai cạnh tương ứng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận