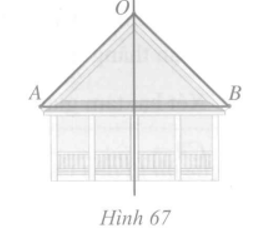
Cho hình thang ABCD có AB song song với CD, AB < CD, AD = BC. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD. Đường thẳng qua I song song với AD cắt đoạn thẳng KD tại M. Đường thẳng qua I song song với BC cắt KC tại N Hình 73. Chứng minh:
a) IM = IN;
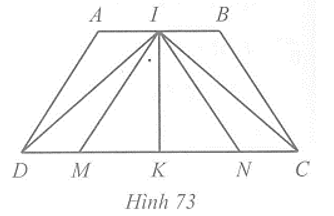
Cho hình thang ABCD có AB song song với CD, AB < CD, AD = BC. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD. Đường thẳng qua I song song với AD cắt đoạn thẳng KD tại M. Đường thẳng qua I song song với BC cắt KC tại N Hình 73. Chứng minh:
a) IM = IN;
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vẽ các đoạn thẳng IC, ID. Xét hai tam giác ADI và MID, ta có
= (hai góc so le trong);
ID là cạnh chung;
= (hai góc so le trong).
Suy ra ∆ADI = ∆MID (g.c.g). Do đó AD = MI, IA = DM (các cặp cạnh tương ứng)
Chứng minh tương tự ta có BC = IN, IB = NC
a) Vì AD = BC, AD = MI, BC = IN nên IM = IN.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
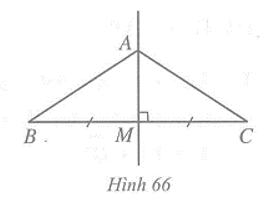
Ta có: = (giả thiết);
+ = 180o (hai góc kề bù)
Suy ra = = 90o
Vậy đường thẳng AM vuông góc với đoạn thẳng BC tại trung điểm M của nó nên AM là đường trung trực của đoạn thẳng BC.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
- Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập