Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc OA, OB, OC hai đường trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 111). Chứng minh:
a) ∆OMA = ∆OMB và tia Om là tia phân giác của góc NMP;
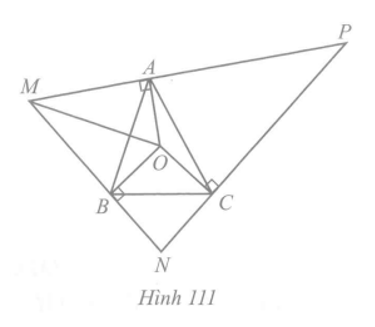
Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc OA, OB, OC hai đường trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 111). Chứng minh:
a) ∆OMA = ∆OMB và tia Om là tia phân giác của góc NMP;

Câu hỏi trong đề: Giải VBT Toán 7 Cánh diều Bài tập cuối chương 7 có đáp án !!
Quảng cáo
Trả lời:
Xét hai tam giác vuông OMA và OMB, ta có:
OM là cạnh chung;
OA = OB (vì O là giao điểm ba đường trung trực của tam giác ABC).
Suy ra ∆OMA = ∆OMB (cạnh huyền – cạnh góc vuông).
Do đó = (hai góc tương ứng).
Vậy tia OM là tia phân giác của góc MNP.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
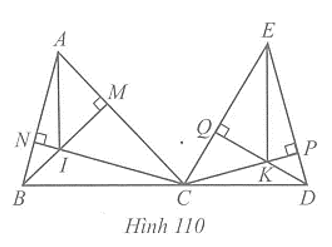
c) Ta có ∆ABD = ∆ACE nên AD = AE (hai cạnh tương ứng).
Xét hai tam giác vuông ADH và AEH, ta có:
AH là cạnh chung; AD = AE.
Suy ra ∆ADH = ∆AEH (cạnh huyền – cạnh góc vuông).
Do = (hai góc tương ứng).
Vậy AH là tia phân giác của góc BAC.
Lời giải
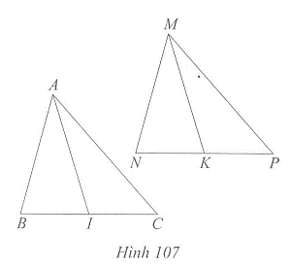
Xét hai tam giác ABC và MNP, ta có:
AB = MN, BC = NP, CA = PM.
Suy ra ∆ABC = ∆MNP (c.c.c).
Do đó = (hai góc tương ứng).
Vì I là trung điểm của BC nên BI = BC
Vì K là trung điểm của NP nên NK = NP
Mà BC = NP, suy ra BI = NK
Xét hai tam giác ABI và MNK, ta có:
AB = MN, = ; BI = NK
Suy ra ∆ABI = ∆MNK (c.g.c)
AI = MK (hai cạnh tương ứng)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.