Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 114). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ điểm D đến điểm A nhỏ nhất? Em hãy giúp Hùng tìm cách vẽ điểm D và giải thích cách làm của mình.
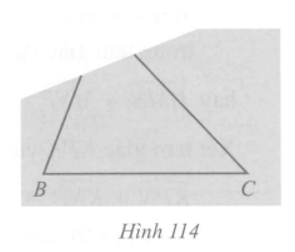
Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 114). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ điểm D đến điểm A nhỏ nhất? Em hãy giúp Hùng tìm cách vẽ điểm D và giải thích cách làm của mình.
Câu hỏi trong đề: Giải VBT Toán 7 Cánh diều Bài tập cuối chương 7 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất nên khoảng cách từ điểm D đến điểm A là nhỏ nhất khi điểm D là hình chiếu của điểm A trên đường thẳng BC.
Suy ra AD là đường cao của tam giác ABC.
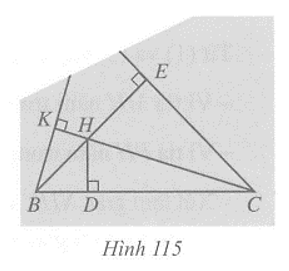
Vẽ hai đường cao BE và CK của tam giác ABC, hai đường cao đó cắt nhau tại H. Khi đó H là trực tâm của tam giác ABC. Suy ra D là hình chiếu của điểm H trên đường thẳng BC (Hình 115).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
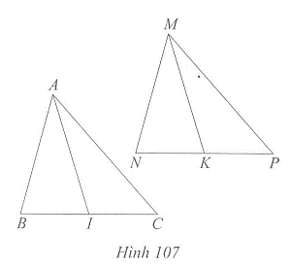
Xét hai tam giác ABC và MNP, ta có:
AB = MN, BC = NP, CA = PM.
Suy ra ∆ABC = ∆MNP (c.c.c).
Do đó = (hai góc tương ứng).
Vì I là trung điểm của BC nên BI = BC
Vì K là trung điểm của NP nên NK = NP
Mà BC = NP, suy ra BI = NK
Xét hai tam giác ABI và MNK, ta có:
AB = MN, = ; BI = NK
Suy ra ∆ABI = ∆MNK (c.g.c)
AI = MK (hai cạnh tương ứng)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
c) Ta có ∆ABD = ∆ACE nên AD = AE (hai cạnh tương ứng).
Xét hai tam giác vuông ADH và AEH, ta có:
AH là cạnh chung; AD = AE.
Suy ra ∆ADH = ∆AEH (cạnh huyền – cạnh góc vuông).
Do = (hai góc tương ứng).
Vậy AH là tia phân giác của góc BAC.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập