Câu hỏi:
30/10/2023 1,361
Tính diện tích của một tam giác cân, biết rằng tam giác đó có hai cạnh với độ dài bằng 4 cm và 8 cm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Vì tam giác cân có hai cạnh là 4 cm và 8 cm nên độ dài cạnh thứ ba của tam giác sẽ là 4 cm hoặc 8 cm.
Mà 4 + 4 = 8 không thỏa mãn bất đẳng thức tam giác nên ta loại trường hợp độ dài ba cạnh là 4 cm, 4 cm, 8 cm.
Do đó, độ dài ba cạnh của tam giác đó là 4 cm, 8 cm, 8 cm.
Giả sử tam giác ABC cân tại A có AB = AC = 8 cm, BC = 4 cm.
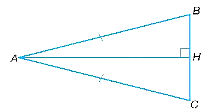
Kẻ đường cao AH (H thuộc BC) của tam giác ABC cân tại A. Khi đó, H là trung điểm của BC nên \(BH = \frac{1}{2}BC\)= 2 cm.
Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có:
AH2 + BH2 = AB2
Suy ra AH2 = AB2 – BH2 = 82 – 22 = 60.
Do đó, AH = \(2\sqrt {15} \) cm.
Diện tích tam giác ABC là: \(\frac{1}{2}AH \cdot BC = \frac{1}{2} \cdot 2\sqrt {15} \cdot 4 = 4\sqrt {15} \) (cm2).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
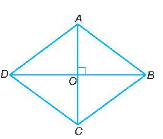
Giả sử hình thoi ABCD có hai đường chéo AC = 6 cm, BD = 8 cm và O là giao điểm của AC và BD. Khi đó, O là trung điểm của AC, O là trung điểm của BD và AC vuông góc với BD tại O.
Suy ra OC = \(\frac{1}{2}\)AC = 3 cm, OD = \(\frac{1}{2}\)BD = 4 cm và \(\widehat {COD} = 90^\circ \).
Do đó, tam giác COD vuông tại O.
Áp dụng định lí Pythagore ta có:
CD2 = OC2 + OD2 = 32 + 42 = 25.
Suy ra CD = 5 cm. Vậy độ dài cạnh của hình thoi là 5 cm.
Lời giải
Lời giải
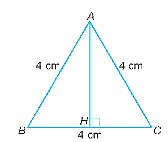
Xét tam giác đều ABC có cạnh AB = AC = BC = 4 cm.
Kẻ đường cao AH của tam giác đều ABC.
Khi đó, đường cao AH đồng thời là đường trung tuyến. Do đó, ta có:
BH = \(\frac{1}{2}\)BC = \(\frac{1}{2}.4\)= 2 (cm).
Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có:
AH2 + BH2 = AB2
Suy ra AH2 = AB2 – BH2 = 42 – 22 = 12.
Do đó, \(AH = \sqrt {12} \) = \(2\sqrt 3 \) (cm).
Diện tích tam giác ABC là: \(\frac{1}{2}AH \cdot BC = \frac{1}{2} \cdot 2\sqrt 3 \cdot 4 = 4\sqrt 3 \) (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận