Giải SBT Toán 8 KNTT Bài 35. Định lý Pythagore và ứng dụng có đáp án

Lời giải

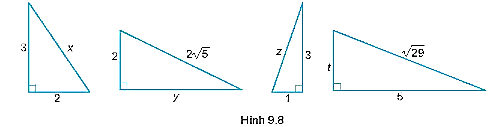
Áp dụng định lý Pythagore vào các tam giác vuông trong Hình 9.8, ta có:

+) x² = 3² + 2² = 9 + 4 = 13 nên x = \(\sqrt {13} \) (đvđd).

+) 2² + y² = \({\left( {2\sqrt 5 } \right)^2}\) nên y² = 20 – 4 = 16, suy ra y = 4 (đvđd).

+) z² = 3² + 1² = 9 + 1 = 10 nên z = \(\sqrt {10} \) (đvđd).

+) t² + 5² = \({\left( {\sqrt {29} } \right)^2}\) nên t² = 29 – 25 = 4 nên t = 2 (đvđd).

Lời giải

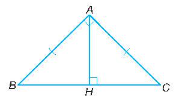
Vì tam giác ABC vuông cân tại A nên

AC = AB = 4 cm

\(\widehat B = \widehat C = 45^\circ \)

Tam giác AHB vuông tại H có \(\widehat B = 45^\circ \), suy ra tam giác AHB vuông cân tại H.

Nên AH = HB.

Tam giác AHC vuông tại H có \(\widehat C = 45^\circ \), suy ra tam giác AHC vuông cân tại H.

Nên AH = HC.

Khi đó, HB = HC = AH.

Mà HB + HC = BC. Suy ra HB + HB = BC hay 2HB = BC.

Do đó, AH = HC = HB = \(\frac{1}{2}\)BC.

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 4² + 4² = 32.

Suy ra BC = \(\sqrt {32} \) = \(4\sqrt 2 \) (cm).

Do đó, AH = \(\frac{1}{2}\)BC = \(2\sqrt 2 \) (cm).

Lời giải

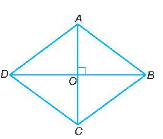
Giả sử hình thoi ABCD có hai đường chéo AC = 6 cm, BD = 8 cm và O là giao điểm của AC và BD. Khi đó, O là trung điểm của AC, O là trung điểm của BD và AC vuông góc với BD tại O.

Suy ra OC = \(\frac{1}{2}\)AC = 3 cm, OD = \(\frac{1}{2}\)BD = 4 cm và \(\widehat {COD} = 90^\circ \).

Do đó, tam giác COD vuông tại O.

Áp dụng định lí Pythagore ta có:

CD² = OC² + OD² = 3² + 4² = 25.

Suy ra CD = 5 cm. Vậy độ dài cạnh của hình thoi là 5 cm.

Lời giải

Xét tam giác ABC vuông tại A.

Áp dụng định lí Pythagore ta có:

AB² + AC² = BC² (1)

Mà \(\frac{{AB}}{{AC}} = \frac{5}{{12}}\) nên AB = \(\frac{5}{{12}}\)AC, thay vào (1) ta có:

\(A{C^2} + {\left( {\frac{5}{{12}}AC} \right)^2} = {26^2}\)

\(\frac{{169}}{{144}}A{C^2} = 676\)

AC² = 576

Suy ra AC = 24 cm.

Do đó, AB = \(\frac{5}{{12}}\).24 = 10 (cm).

Lời giải

Vì AD là đường cao của tam giác ABC nên AD vuông góc với BC.

Do đó, \(\widehat {ADB} = \widehat {ADC} = 90^\circ \).

Tam giác ABD và tam giác CAD có:

\(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (cmt)

\(\widehat {BAD} = \widehat C\) (cùng phụ với góc DAC).

Do đó, ∆ABD ᔕ ∆CAD (g.g).

Suy ra \(\frac{{AD}}{{CD}} = \frac{{BD}}{{AD}}\) nên AD² = CD . BD = 8 . 2 = 16.

Do đó, AD = 4 cm.

Áp dụng định lý Pythagore trong tam giác vuông ABD vuông tại D có:

AB² = AD² + BD² = 4² + 2² = 20.

Nên AB = \(2\sqrt 5 \)cm.

Áp dụng định lý Pythagore vào tam giác ACD vuông tại D có:

AC² = AD² + CD² = 4² + 8² = 80.

Nên AC = \(4\sqrt 5 \) cm.

Lời giải

Giả sử tam giác ABC vuông tại A có: AB : AC = 3 : 4 và chu vi tam giác bằng 48 cm.

Vì AB : AC = 3 : 4 nên AB = \(\frac{3}{4}\)AC.

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có:

BC² = AB² + AC² = \({\left( {\frac{3}{4}AC} \right)^2} + A{C^2} = \frac{{25}}{{16}}A{C^2}\)

Nên BC = \(\frac{5}{4}AC\).

Chu vi tam giác ABC là:

AB + BC + AC = 48

\(AC + \frac{3}{4}AC + \frac{5}{4}AC = 48\)

3AC = 48

AC = 16 (cm)

Do đó, BC = \(\frac{5}{4}AC\) = \(\frac{5}{4}.16\) = 20 (cm).

Lời giải

Vì tam giác cân có hai cạnh là 4 cm và 8 cm nên độ dài cạnh thứ ba của tam giác sẽ là 4 cm hoặc 8 cm.

Mà 4 + 4 = 8 không thỏa mãn bất đẳng thức tam giác nên ta loại trường hợp độ dài ba cạnh là 4 cm, 4 cm, 8 cm.

Do đó, độ dài ba cạnh của tam giác đó là 4 cm, 8 cm, 8 cm.

Giả sử tam giác ABC cân tại A có AB = AC = 8 cm, BC = 4 cm.

Kẻ đường cao AH (H thuộc BC) của tam giác ABC cân tại A. Khi đó, H là trung điểm của BC nên \(BH = \frac{1}{2}BC\)= 2 cm.

Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có:

AH² + BH² = AB²

Suy ra AH² = AB² – BH² = 8² – 2² = 60.

Do đó, AH = \(2\sqrt {15} \) cm.

Diện tích tam giác ABC là: \(\frac{1}{2}AH \cdot BC = \frac{1}{2} \cdot 2\sqrt {15} \cdot 4 = 4\sqrt {15} \) (cm²).

Lời giải

Xét tam giác đều ABC có cạnh AB = AC = BC = 4 cm.

Kẻ đường cao AH của tam giác đều ABC.

Khi đó, đường cao AH đồng thời là đường trung tuyến. Do đó, ta có:

BH = \(\frac{1}{2}\)BC = \(\frac{1}{2}.4\)= 2 (cm).

Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có:

AH² + BH² = AB²

Suy ra AH² = AB² – BH² = 4² – 2² = 12.

Do đó, \(AH = \sqrt {12} \) = \(2\sqrt 3 \) (cm).

Diện tích tam giác ABC là: \(\frac{1}{2}AH \cdot BC = \frac{1}{2} \cdot 2\sqrt 3 \cdot 4 = 4\sqrt 3 \) (cm²).

Lời giải

Gọi chiều cao màn hình ti vi là h (cm).

Áp dụng định lý Pythagore cho tam giác vuông với hai cạnh góc vuông là hai cạnh của màn hình chiếc ti vi.

Khi đó, cạnh huyền của tam giác vuông này có độ dài bằng: 32 . 2,54 = 81,28 (cm).

Áp dụng định lý Pythagore cho tam giác vuông ta suy ra:

h² = 81,28² – 72² = 1 422,4384

Suy ra h = \(\sqrt {1422,4384} \) ≈ 37,72 (cm).