Câu hỏi:
24/08/2024 5,402
Công thức \(E = \frac{1}{2}m{v^2}\) (J) được dùng để tính động năng của một vật có khối lượng m (kg) khi chuyển động với vận tốc v (m/s) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
a) Giả sử một quả bóng có khối lượng 2 kg đang bay với vận tốc 6 m/s. Tính động năng của quả bóng đó.
b) Giả sử động năng của quả bóng đang bay có khối lượng 1,5 kg là 48 J, hãy tính vận tốc bay của quả bóng đó.
Công thức \(E = \frac{1}{2}m{v^2}\) (J) được dùng để tính động năng của một vật có khối lượng m (kg) khi chuyển động với vận tốc v (m/s) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
a) Giả sử một quả bóng có khối lượng 2 kg đang bay với vận tốc 6 m/s. Tính động năng của quả bóng đó.
b) Giả sử động năng của quả bóng đang bay có khối lượng 1,5 kg là 48 J, hãy tính vận tốc bay của quả bóng đó.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung chương 6 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Với m = 2 kg và v = 6 m/s, ta có: \(E = \frac{1}{2}{.2.6^2} = 36\) (J).
Vậy động năng của quả bóng là 36 J.
b) Với m = 1,5 kg và E = 48 J, ta có: \(48 = \frac{1}{2}.1,5.{v^2},\) suy ra v2 = 64 hay v = 8 (do v > 0). Vậy vận tốc bay của quả bóng là 8 m/s.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Parabol đi qua điểm \(A\left( {2;4\sqrt 3 } \right)\) nên ta có \(4\sqrt 3 = a{.2^2} = 4a\) suy ra \(a = \sqrt 3 .\)
Từ đó, vẽ được đồ thị của hàm số \(y = \sqrt 3 {x^2}\) như hình bên:
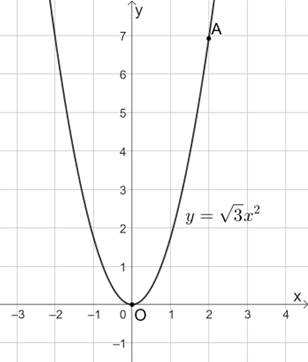
b) Tung độ của điểm thuộc parabol có hoành độ x = −1 là \(y = \sqrt 3 .\left( { - 1} \right) = - \sqrt 3 .\)
c) Tọa độ điểm thuộc parabol có tung độ \(y = 5\sqrt 3 \) thỏa mãn \(5\sqrt 3 = \sqrt 3 {x^2},\) hay x2 = 5, suy ra \(x = \sqrt 5 \) hoặc \(x = - \sqrt 5 .\)
Vậy có hai điểm cần tìm là \(\left( {\sqrt 5 ;5\sqrt 3 } \right)\) và \(\left( { - \sqrt 5 ;5\sqrt 3 } \right).\)
Lời giải
Gọi độ dài cạnh của tấm tôn hình vuông ban đầu là x (cm). Điều kiện: x > 16.
Theo cách gập thì độ dài cạnh bên của chiếc thùng là 8 (cm) và độ dài hai cạnh đáy của chiếc thùng đều là x – 2.8 = x – 16 (cm).
Do đó, thể tích của chiếc thùng có dạng hình hộp chữ nhật là: 8.(x – 16)2 (cm3).
Do thể tích của hộp là 200 cm3 nên ta có phương trình:
8.(x – 16)2 = 200
(x – 16)2 = 25
x – 16 = 5 hoặc x – 16 = −5
x = 21 hoặc x = 11.
Vì điều kiện x > 16 nên ta chọn x = 21.
Vậy độ dài cạnh của tấm tôn hình vuông ban đầu là 21 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)