a) Parabol đi qua điểm \(A\left( {2;4\sqrt 3 } \right)\) nên ta có \(4\sqrt 3 = a{.2^2} = 4a\) suy ra \(a = \sqrt 3 .\)

Từ đó, vẽ được đồ thị của hàm số \(y = \sqrt 3 {x^2}\) như hình bên:

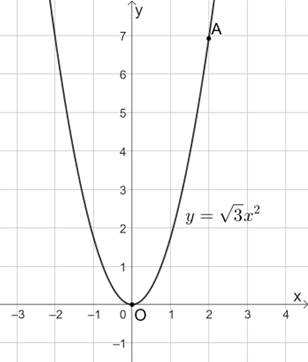
b) Tung độ của điểm thuộc parabol có hoành độ x = −1 là \(y = \sqrt 3 .\left( { - 1} \right) = - \sqrt 3 .\)

c) Tọa độ điểm thuộc parabol có tung độ \(y = 5\sqrt 3 \) thỏa mãn \(5\sqrt 3 = \sqrt 3 {x^2},\) hay x² = 5, suy ra \(x = \sqrt 5 \) hoặc \(x = - \sqrt 5 .\)

Vậy có hai điểm cần tìm là \(\left( {\sqrt 5 ;5\sqrt 3 } \right)\) và \(\left( { - \sqrt 5 ;5\sqrt 3 } \right).\)

a) Với m = 2 kg và v = 6 m/s, ta có: \(E = \frac{1}{2}{.2.6^2} = 36\) (J).

Vậy động năng của quả bóng là 36 J.

b) Với m = 1,5 kg và E = 48 J, ta có: \(48 = \frac{1}{2}.1,5.{v^2},\) suy ra v² = 64 hay v = 8 (do v > 0). Vậy vận tốc bay của quả bóng là 8 m/s.

a) Áp dụng định lí Pythagore, ta tính được chiều cao của tam giác đều cạnh a là

\({h_1} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \sqrt {\frac{{3{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\) (cm).

Diện tích đáy S của hình chóp là \(S = \frac{1}{2}a.{h_1} = \frac{1}{2}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{4}\) (cm²).

b) Thể tích của hình chóp tam giác đều là

\(V = \frac{1}{3}S.h = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.10 = \frac{{5\sqrt 3 }}{6}{a^2}\) (cm³).

c) Chiều cao mới của đáy là

\({h_{moi}} = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} - {{\left( {\frac{a}{4}} \right)}^2}} = \sqrt {\frac{{{a^2}}}{4} - \frac{{{a^2}}}{{16}}} = \frac{{a\sqrt 3 }}{4}\) (cm).

Diện tích đáy mới là \({S_{moi}} = \frac{1}{2}.\frac{a}{2}.\frac{{a\sqrt 3 }}{4} = \frac{1}{4}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{1}{4}{S_{cu}}.\)

Suy ra \({V_{moi}} = \frac{1}{3}{S_{moi}}.h = \frac{1}{3}.\frac{1}{4}{S_{cu}}.h = \frac{1}{4}{V_{cu}}.\)

Vậy nếu độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp giảm đi 4 lần.

a) Ta có: \(\Delta ' = {\left( { - \sqrt 5 } \right)^2} - 1.1 = 4 > 0.\)

Áp dụng công thức nghiệm thu gọn, phương trình có hai nghiệm phân biệt:

\({x_1} = \sqrt 5 + 2,\) \({x_2} = \sqrt 5 - 2.\)

b) Ta có: \(\Delta = {\left( { - 9} \right)^2} - 4.3.3 = 45 > 0,\) \(\sqrt \Delta   = 3\sqrt 5 .\)

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt:

\({x_1} = \frac{{9 + 3\sqrt 5 }}{6} = \frac{{3 + \sqrt 5 }}{2},\) \({x_2} = \frac{{9 - 3\sqrt 5 }}{6} = \frac{{3 - \sqrt 5 }}{2}.\)

c) Ta có: \(\Delta = {\left( { - 13} \right)^2} - 4.11.5 = - 51 < 0.\)

Do đó, phương trình vô nghiệm.

d) Ta có: \(\Delta ' = {\left( {\sqrt 6 } \right)^2} - 2.3 = 0.\)

Áp dụng công thức nghiệm thu gọn, phương trình có nghiệm kép:

\({x_1} = {x_2} = \frac{{ - \sqrt 6 }}{2}.\)

a) Sử dụng máy tính cầm tay, phương trình có hai nghiệm phân biệt:

\({x_1} \approx 1,94;\) \({x_2} \approx - 0,36.\)

b) Sử dụng máy tính cầm tay, phương trình có hai nghiệm phân biệt:

\({x_1} \approx 2,03;\) \({x_2} \approx - 1,3.\)

Gọi độ dài cạnh của tấm tôn hình vuông ban đầu là x (cm). Điều kiện: x > 16.

Theo cách gập thì độ dài cạnh bên của chiếc thùng là 8 (cm) và độ dài hai cạnh đáy của chiếc thùng đều là x – 2.8 = x – 16 (cm).

Do đó, thể tích của chiếc thùng có dạng hình hộp chữ nhật là: 8.(x – 16)² (cm³).

Do thể tích của hộp là 200 cm³ nên ta có phương trình:

8.(x – 16)² = 200

(x – 16)² = 25

x – 16 = 5 hoặc x – 16 = −5

x = 21 hoặc x = 11.

Vì điều kiện x > 16 nên ta chọn x = 21.

Vậy độ dài cạnh của tấm tôn hình vuông ban đầu là 21 cm.