Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình sau:
a) \({x^2} - 2\sqrt 5 x + 1 = 0;\)
b) 3x2 – 9x + 3 = 0;
c) 11x2 – 13x + 5 = 0;
d) \(2{x^2} + 2\sqrt 6 x + 3 = 0.\)
Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình sau:
a) \({x^2} - 2\sqrt 5 x + 1 = 0;\)
b) 3x2 – 9x + 3 = 0;
c) 11x2 – 13x + 5 = 0;
d) \(2{x^2} + 2\sqrt 6 x + 3 = 0.\)
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung chương 6 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có: \(\Delta ' = {\left( { - \sqrt 5 } \right)^2} - 1.1 = 4 > 0.\)
Áp dụng công thức nghiệm thu gọn, phương trình có hai nghiệm phân biệt:
\({x_1} = \sqrt 5 + 2,\) \({x_2} = \sqrt 5 - 2.\)
b) Ta có: \(\Delta = {\left( { - 9} \right)^2} - 4.3.3 = 45 > 0,\) \(\sqrt \Delta = 3\sqrt 5 .\)
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{9 + 3\sqrt 5 }}{6} = \frac{{3 + \sqrt 5 }}{2},\) \({x_2} = \frac{{9 - 3\sqrt 5 }}{6} = \frac{{3 - \sqrt 5 }}{2}.\)
c) Ta có: \(\Delta = {\left( { - 13} \right)^2} - 4.11.5 = - 51 < 0.\)
Do đó, phương trình vô nghiệm.
d) Ta có: \(\Delta ' = {\left( {\sqrt 6 } \right)^2} - 2.3 = 0.\)
Áp dụng công thức nghiệm thu gọn, phương trình có nghiệm kép:
\({x_1} = {x_2} = \frac{{ - \sqrt 6 }}{2}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Với m = 2 kg và v = 6 m/s, ta có: \(E = \frac{1}{2}{.2.6^2} = 36\) (J).
Vậy động năng của quả bóng là 36 J.
b) Với m = 1,5 kg và E = 48 J, ta có: \(48 = \frac{1}{2}.1,5.{v^2},\) suy ra v2 = 64 hay v = 8 (do v > 0). Vậy vận tốc bay của quả bóng là 8 m/s.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Parabol đi qua điểm \(A\left( {2;4\sqrt 3 } \right)\) nên ta có \(4\sqrt 3 = a{.2^2} = 4a\) suy ra \(a = \sqrt 3 .\)
Từ đó, vẽ được đồ thị của hàm số \(y = \sqrt 3 {x^2}\) như hình bên:
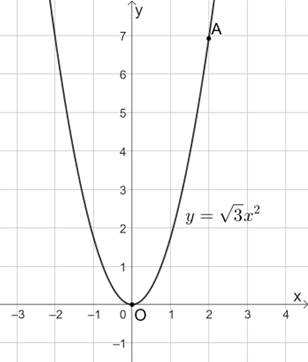
b) Tung độ của điểm thuộc parabol có hoành độ x = −1 là \(y = \sqrt 3 .\left( { - 1} \right) = - \sqrt 3 .\)
c) Tọa độ điểm thuộc parabol có tung độ \(y = 5\sqrt 3 \) thỏa mãn \(5\sqrt 3 = \sqrt 3 {x^2},\) hay x2 = 5, suy ra \(x = \sqrt 5 \) hoặc \(x = - \sqrt 5 .\)
Vậy có hai điểm cần tìm là \(\left( {\sqrt 5 ;5\sqrt 3 } \right)\) và \(\left( { - \sqrt 5 ;5\sqrt 3 } \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập