Một bể chứa 2 m³ nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ không đổi với tốc độ 20 lít/phút. Biết rằng nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số f(t), thời gian t tính bằng phút. Biết rằng tiệm cận ngang của đồ thị hàm số f(t) là y = 19. Nồng độ muối trong bể sau khi bơm được 1 giờ là bao nhiêu?

Đáp án đúng là: A

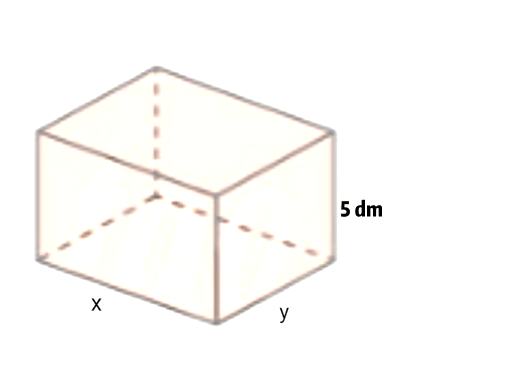
Do thể tích của bể là 1 m³ nên 0,5xy = 1 $\iff$ xy = 2 .

Diện tích toàn phần của bể là \(S\left( x \right) = xy + 2.0,5.x + 2.0,5.y = 2 + x + \frac{2}{x},\,\,\,\,\left( {x > 0} \right)\).

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left( {S\left( x \right) - \left( {x + 2} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x} = 0\).

Suy ra đồ thị hàm số S(x) có đường tiệm cận xiên là y = x + 2 $\Rightarrow$ a = 1; b = 2.

Vậy P = a² + b² = 5.

Đáp án đúng là: B

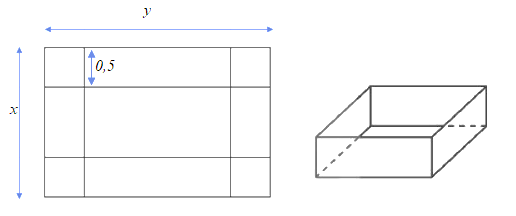
Do tấm tôn có diện tích bằng 4 m² nên \(xy = 4 \Leftrightarrow y = \frac{4}{x}\)

Thùng có chiều cao là 0,5 m và các kích thước còn lại của thùng là: x – 1 và y – 1.

Thể tích của thùng là \(V\left( x \right) = 0,5.\left( {x - 1} \right)\left( {y - 1} \right) = \frac{1}{2}\left( {x - 1} \right)\left( {\frac{4}{x} - 1} \right) = \frac{1}{2}\frac{{\left( {x - 1} \right)\left( {4 - x} \right)}}{x}\)

Suy ra: \(y = \frac{1}{{V\left( x \right)}} = \frac{{2x}}{{\left( {x - 1} \right)\left( {4 - x} \right)}}\).

Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{V\left( x \right)}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x}}{{\left( {x - 1} \right)\left( {4 - x} \right)}} = + \infty \) và \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{1}{{V\left( x \right)}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{2x}}{{\left( {x - 1} \right)\left( {4 - x} \right)}} = - \infty \)

Suy ra đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số \(y = \frac{1}{{V\left( x \right)}}\).

\(\mathop {\lim }\limits_{x \to {4^ + }} \frac{1}{{V\left( x \right)}} = \mathop {\lim }\limits_{x \to {4^ + }} \frac{{2x}}{{\left( {x - 1} \right)\left( {4 - x} \right)}} = - \infty \) và \(\mathop {\lim }\limits_{x \to {4^ - }} \frac{1}{{V\left( x \right)}} = \mathop {\lim }\limits_{x \to {4^ - }} \frac{{2x}}{{\left( {x - 1} \right)\left( {4 - x} \right)}} = + \infty \)

Suy ra đường thẳng x = 4 là đường tiệm cận đứng của đồ thị hàm số \(y = \frac{1}{{V\left( x \right)}}\).

Vậy đồ thị hàm số \(y = \frac{1}{{V\left( x \right)}}\) có 2 đường tiệm cận đứng.