Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình \(v(\;{\rm{km}}/{\rm{h}})\) theo công thức:
\(C(v) = \frac{{16000}}{v} + \frac{5}{2}v(0 < v \le 120)\)
Để biểu diễn trực quan sự thay đổi của \(C(v)\) theo \(v\), người ta đã vẽ đổ thị hàm số \(C(v)\) như hình bên dưới.
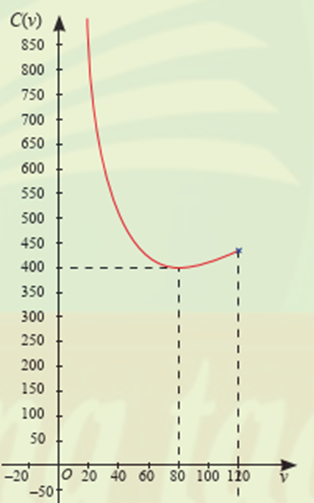
a) Khảo sát và vẽ đồ thị hàm số \(C(v)\) trên \((0;120]\).
b) Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?
Quảng cáo
Trả lời:
a) Khảo sát và vẽ đồ thị của hàm số \(C(v)\) :
Tập xác định: \(D = (0;120]\).
Sự biến thiên:
Chiều biến thiên:
Đạo hàm \({C^\prime }(v) = - \frac{{16000}}{{{v^2}}} + \frac{5}{2} = \frac{{5(v - 80)(v + 80)}}{{2{v^2}}};{C^\prime }(v) = 0 \Leftrightarrow v = - 80\) (loại) hoặc \(v = 80\).
Trên khoảng \((0;80),{C^\prime }(v) < 0\) nên hàm số nghịch biến trên khoảng này.
Trên khoảng \((80;120),{C^\prime }(v) > 0\) nên hàm số đồng biến trên khoảng này.
Cực trị: Hàm số đạt cực tiểu tại \(v = 80,{C_{CT}} = C(80) = 400\).
Giới hạn vô cực và tiệm cận: \(\mathop {\lim }\limits_{v \to {0^ + }} C(v) = \mathop {\lim }\limits_{v \to {0^ + }} \left( {\frac{{16000}}{v} + \frac{5}{2}v} \right) = + \infty \) nên đường thẳng \(v = 0\) là tiệm cận đứng của đồ thị hàm số.
Bảng biến thiên:
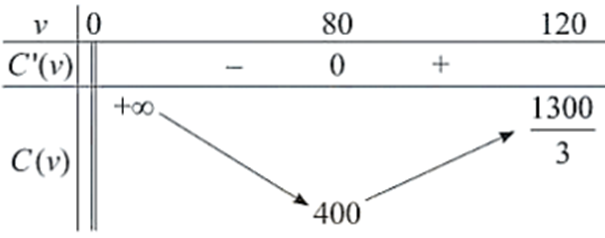
Đồ thị:
Đồ thị hàm số có điểm cực tiểu \((80;400)\) và đi qua các điểm \((40;500),(100;410),\left( {120;\frac{{1300}}{3}} \right)\).
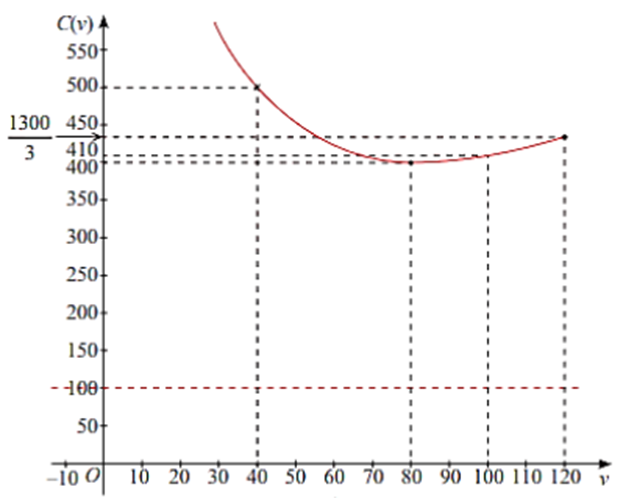
b) Quan sát đồ thị hàm số, ta nhận thấy hàm số đạt GTNN khi \(v = 80\) và GTNN là 400 .
Như vậy, để tiết kiệm tiền xăng nhất, tài xế nên chạy xe với tốc độ trung bình là \(80\;{\rm{km}}/{\rm{h}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
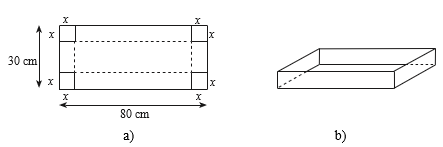
Thể tích chiếc hộp là: V(x) = x(30 – 2x)(80 – 2x) = 2 400x – 220x2 + 4x3 với 5 ≤ x ≤ 10.
Ta có: V '(x) = 12x2 – 440x + 2 400;
V '(x) = 0 ⇔ x = hoặc x = 30 (loại vì không thuộc [5; 10]);
V(5) = 7 000; \[V\left( {\frac{{20}}{3}} \right) = \frac{{200000}}{{27}}\]; V(10) = 6 000.
Do đó \[\mathop {\max }\limits_{\left[ {5;10} \right]} V\left( x \right) = \frac{{200000}}{{27}}{\rm{ khi x = }}\frac{{20}}{3}\]
Vậy để thể tích chiếc hộp là lớn nhất thì x = \[\frac{{20}}{3}\] cm.
Lời giải
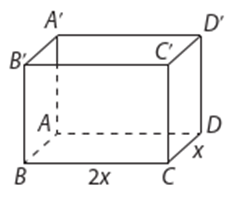
Xem bể chứa có dạng hình hộp chữ nhật ABCD.A’B’C’D’ như hình vẽ trên
Gọi x (m) là chiều rộng của bể, ta có \[0 < x \le 4\].
Chiều dài của bể là 2x (m).
Gọi h (m) là chiều cao bể nước, ta có thể tích của bể là V = x.(2x).h.
Suy ra: \[h = \frac{V}{{2{x^2}}} = \frac{{36}}{{2{x^2}}} = \frac{{18}}{{{x^2}}}{\rm{ }}(m)\]
Tổng diện tích các mặt cần xây là:
\[S = {S_{ABCD}} + 2{S_{ABB'A'}} + 2{S_{BCC'B'}} = 2{x^2} + 2.x.\frac{{18}}{{{x^2}}} + 2.2x.\frac{{18}}{{{x^2}}} = 2{x^2} + \frac{{108}}{x}\]
Xét hàm số \[S(x) = 2{x^2} + \frac{{108}}{x}(0 < x \le 4)\], ta có: \[S'(x) = 4x - \frac{{108}}{{{x^2}}} = \frac{{4{x^3} - 108}}{{{x^2}}} = \frac{{4(x - 3)({x^2} + 3x + 9)}}{{{x^2}}}\]
\[S'(x) = 0 \Leftrightarrow x = 3\]
Bảng biến thiên:
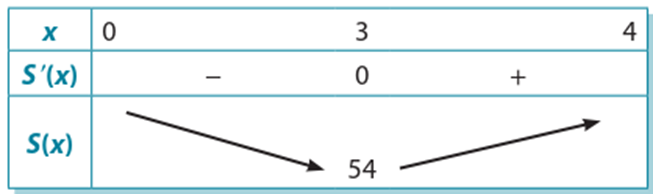
Chi phí vật liệu xây dựng thấp nhất khi tổng diện tích các mặt cần xây S(x) là nhỏ nhất.
Dựa vào bảng biến thiên, ta có S(x) đạt giá trị nhỏ nhất tại x = 3, suy ra h = 2.
Vậy cần xây bể có chiều cao là 2 (m).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.