Ho ép khí quản co lại, ảnh hưởng đến tốc độ của không khí đi vào khí quản. Tốc độ của không khí đi vào khí quản khi họ được cho bởi công thức: V = k(R-r)r2 vôi 0 ≤ r <R, trong đó k là hằng số, R là bán kính bình thường của khí quản, r là bán kính khí quản khi ho (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất?
Ho ép khí quản co lại, ảnh hưởng đến tốc độ của không khí đi vào khí quản. Tốc độ của không khí đi vào khí quản khi họ được cho bởi công thức: V = k(R-r)r2 vôi 0 ≤ r <R, trong đó k là hằng số, R là bán kính bình thường của khí quản, r là bán kính khí quản khi ho (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất?
Quảng cáo
Trả lời:
Xét hàm số \(V = k(R - r){r^2}\) với \(r \in [0;R)\)
Ta có \(V(r) = k \cdot \left( { - {r^2}} \right) + k(R - r) \cdot 2r = rk(2R - 3r)\).
Khi đó, trên nửa khoảng \([0;{\rm{R}}),{\rm{V}}({\rm{r}}) = 0\) khi \({\rm{r}} = 0\) hoặc \({\rm{r}} = \frac{2}{3}R\).
Bảng biến thiên của hàm số như sau:
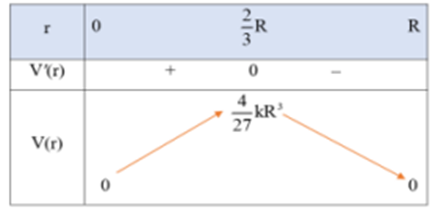
Từ bảng biến thiên, ta thấy \({\max _{[0,R)}}{\rm{V}} = \frac{4}{{27}}k{R^3}\) tại \({\rm{r}} = \frac{2}{3}R\).
Vậy \({\rm{r}} = \frac{2}{3}R\) thì tốc độ của không khí đi vào khí quản là lớn nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
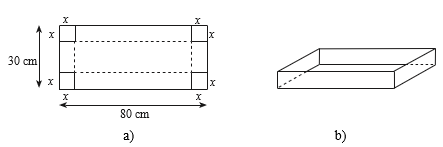
Thể tích chiếc hộp là: V(x) = x(30 – 2x)(80 – 2x) = 2 400x – 220x2 + 4x3 với 5 ≤ x ≤ 10.
Ta có: V '(x) = 12x2 – 440x + 2 400;
V '(x) = 0 ⇔ x = hoặc x = 30 (loại vì không thuộc [5; 10]);
V(5) = 7 000; \[V\left( {\frac{{20}}{3}} \right) = \frac{{200000}}{{27}}\]; V(10) = 6 000.
Do đó \[\mathop {\max }\limits_{\left[ {5;10} \right]} V\left( x \right) = \frac{{200000}}{{27}}{\rm{ khi x = }}\frac{{20}}{3}\]
Vậy để thể tích chiếc hộp là lớn nhất thì x = \[\frac{{20}}{3}\] cm.
Lời giải
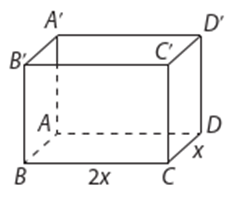
Xem bể chứa có dạng hình hộp chữ nhật ABCD.A’B’C’D’ như hình vẽ trên
Gọi x (m) là chiều rộng của bể, ta có \[0 < x \le 4\].
Chiều dài của bể là 2x (m).
Gọi h (m) là chiều cao bể nước, ta có thể tích của bể là V = x.(2x).h.
Suy ra: \[h = \frac{V}{{2{x^2}}} = \frac{{36}}{{2{x^2}}} = \frac{{18}}{{{x^2}}}{\rm{ }}(m)\]
Tổng diện tích các mặt cần xây là:
\[S = {S_{ABCD}} + 2{S_{ABB'A'}} + 2{S_{BCC'B'}} = 2{x^2} + 2.x.\frac{{18}}{{{x^2}}} + 2.2x.\frac{{18}}{{{x^2}}} = 2{x^2} + \frac{{108}}{x}\]
Xét hàm số \[S(x) = 2{x^2} + \frac{{108}}{x}(0 < x \le 4)\], ta có: \[S'(x) = 4x - \frac{{108}}{{{x^2}}} = \frac{{4{x^3} - 108}}{{{x^2}}} = \frac{{4(x - 3)({x^2} + 3x + 9)}}{{{x^2}}}\]
\[S'(x) = 0 \Leftrightarrow x = 3\]
Bảng biến thiên:
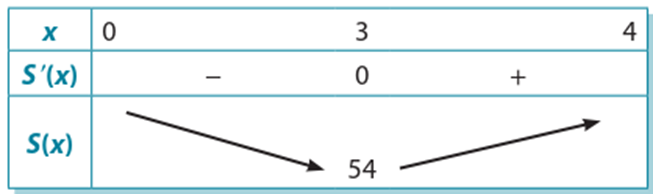
Chi phí vật liệu xây dựng thấp nhất khi tổng diện tích các mặt cần xây S(x) là nhỏ nhất.
Dựa vào bảng biến thiên, ta có S(x) đạt giá trị nhỏ nhất tại x = 3, suy ra h = 2.
Vậy cần xây bể có chiều cao là 2 (m).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.