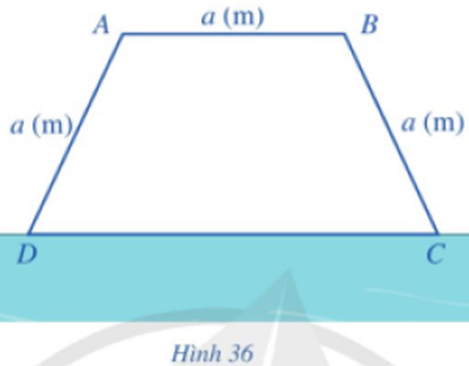
Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài a (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD như Hình 36 (bờ sông là đường thẳng CD không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?

Quảng cáo
Trả lời:
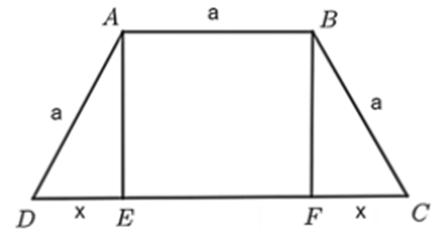
Dựng các đường cao AE và BF của hình thang cân ABCD như hình vẽ trên.
Vi ABCD là hình thang cân nên \(DE = FC\) và \(EF = AB = a\).
Đặt \({\rm{DE}} = {\rm{FC}} = {\rm{x}}({\rm{m}})({\rm{x}} > 0)\).
Ta có \({\rm{DC}} = {\rm{DE}} + {\rm{EF}} + {\rm{FC}} = {\rm{x}} + {\rm{a}} + {\rm{x}} = 2{\rm{x}} + {\rm{a}}\).
Theo định lí Pythagore, ta suy ra \({\rm{AE}} = \sqrt {A{D^2} - D{E^2}} = \sqrt {{a^2} - {x^2}} (\;{\rm{m}})\).
Rõ ràng, \({\rm{x}}\) phải thỏa mãn điều kiện \(0 < x < a\).
Diện tích của hình thang cân ABCD là:
\({\rm{S}} = \frac{1}{2}({\rm{AB}} + {\rm{CD}}){\rm{AE}} = \frac{1}{2}({\rm{a}} + 2{\rm{x}} + {\rm{a}})\sqrt {{a^2} - {x^2}} = ({\rm{a}} + {\rm{x}})\sqrt {{a^2} - {x^2}} \left( {\;{{\rm{m}}^2}} \right){\rm{. }}\)
Xét hàm số \({\rm{S}}({\rm{x}}) = ({\rm{a}} + {\rm{x}})\sqrt {{a^2} - {x^2}} \) với \({\rm{x}} \in (0;{\rm{a}})\).
Ta có \(S(x) = \frac{{ - 2{x^2} - ax + {a^2}}}{{\sqrt {{a^2} - {x^2}} }}\);
\(S(x) = 0 \Leftrightarrow - 2{x^2} - ax + {a^2} = 0 \Leftrightarrow (x + a)(a - 2x) = 0 \Leftrightarrow x = - {\rm{ a hoac }}x = \frac{a}{2}{\rm{. }}\)
Khi đó trên khoảng \((0;a),S(x) = 0\) khi \({\rm{x}} = \frac{a}{2}\).
Bảng biến thiên của hàm số \(S(x)\) như sau:
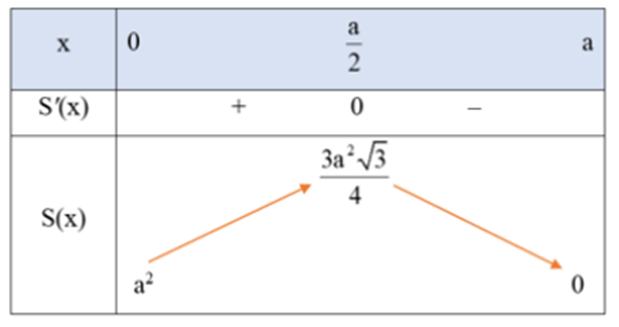
Căn cứ vào bảng biến thiên, ta thấy hàm số \({\rm{S}}({\rm{x}})\) đạt giá trị lớn nhất bằng \(\frac{{3{a^2}\sqrt 3 }}{4}\) tại \(x = \frac{a}{2}\).
Vậy bác đó có thề rào được mảnh vườn có diện tích lớn nhắt là \(\frac{{3{a^2}\sqrt 3 }}{4}\left( {\;{{\rm{m}}^2}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
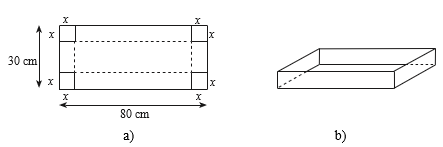
Thể tích chiếc hộp là: V(x) = x(30 – 2x)(80 – 2x) = 2 400x – 220x2 + 4x3 với 5 ≤ x ≤ 10.
Ta có: V '(x) = 12x2 – 440x + 2 400;
V '(x) = 0 ⇔ x = hoặc x = 30 (loại vì không thuộc [5; 10]);
V(5) = 7 000; \[V\left( {\frac{{20}}{3}} \right) = \frac{{200000}}{{27}}\]; V(10) = 6 000.
Do đó \[\mathop {\max }\limits_{\left[ {5;10} \right]} V\left( x \right) = \frac{{200000}}{{27}}{\rm{ khi x = }}\frac{{20}}{3}\]
Vậy để thể tích chiếc hộp là lớn nhất thì x = \[\frac{{20}}{3}\] cm.
Lời giải
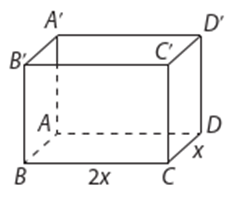
Xem bể chứa có dạng hình hộp chữ nhật ABCD.A’B’C’D’ như hình vẽ trên
Gọi x (m) là chiều rộng của bể, ta có \[0 < x \le 4\].
Chiều dài của bể là 2x (m).
Gọi h (m) là chiều cao bể nước, ta có thể tích của bể là V = x.(2x).h.
Suy ra: \[h = \frac{V}{{2{x^2}}} = \frac{{36}}{{2{x^2}}} = \frac{{18}}{{{x^2}}}{\rm{ }}(m)\]
Tổng diện tích các mặt cần xây là:
\[S = {S_{ABCD}} + 2{S_{ABB'A'}} + 2{S_{BCC'B'}} = 2{x^2} + 2.x.\frac{{18}}{{{x^2}}} + 2.2x.\frac{{18}}{{{x^2}}} = 2{x^2} + \frac{{108}}{x}\]
Xét hàm số \[S(x) = 2{x^2} + \frac{{108}}{x}(0 < x \le 4)\], ta có: \[S'(x) = 4x - \frac{{108}}{{{x^2}}} = \frac{{4{x^3} - 108}}{{{x^2}}} = \frac{{4(x - 3)({x^2} + 3x + 9)}}{{{x^2}}}\]
\[S'(x) = 0 \Leftrightarrow x = 3\]
Bảng biến thiên:
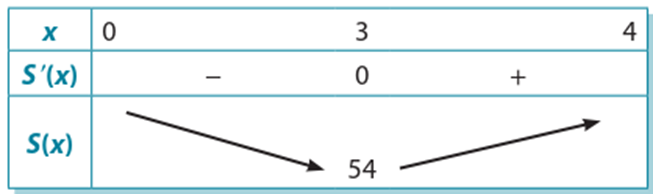
Chi phí vật liệu xây dựng thấp nhất khi tổng diện tích các mặt cần xây S(x) là nhỏ nhất.
Dựa vào bảng biến thiên, ta có S(x) đạt giá trị nhỏ nhất tại x = 3, suy ra h = 2.
Vậy cần xây bể có chiều cao là 2 (m).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.